1、线性性
【元件的线性性】当描述元件的特性方程为线性方程时，元件为线性元件，如线性电阻元件有
的特性方程，线性受控源（CCVS）
。
【线性电路】 除独立电源外，电路中的其他元件均为线性元件，这种电路称为线性电路
【线性时不变电路】除独立电源外，电路中其他元件均为线性元件，且是时不变元件，这种电路称为线性时不变电路。
【电路的线性性】线性电路中，响应（电路中的任何电压或电流）和激励（独立电压源与独立电流源）的关系为线性关系。线性关系体现为可加性和齐次性。
【齐次性】 在仅有一个独立电源激励的线性电路中，若将激励增大K倍，响应也相应增大K倍，如图4-1-1所示，如果
激励下的某个响应（电路中的任何电压或电流）为
，则
激励下的某个响应为
。
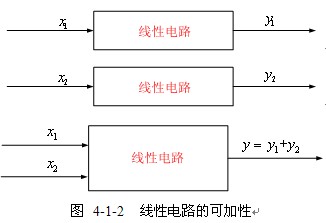
【可加性】 多个激励共同作用引起的响应，等于每个激励单独作用所引起的响应之和。如图4-1-2所示，如果
激励下的某个响应为
，
激励下的某个响应为
，则和共同激励下的响应为
。
2、叠加定理
【叠加定理】 对于任意线性电路，由多个独立电源共同作用所引起的响应等于这些独立电源分别单独作用时所引起的响应的代数和。叠加定理是线性电路的线性性质的体现。
【例4-1-1】 应用叠加定理计算图4-1-3（a）中电流
和电压
。
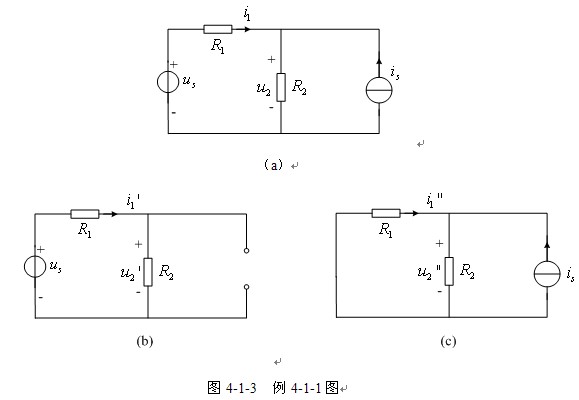
解 图4-1-3（a）所示电路有一个独立电压源和一个独立电流源，两个电源共同作用下的响应可以由结点分析方程求得。即
解得 
则电流为 
通过叠加定理分析。独立电源分别单独作用的电路如图4-1-3（b）、（c）所示。电压源
单独作用电路如图4-1-4（b）所示，有
，
电流源
单独作用电路如图4-1-3（c）所示，有
，
根据叠加定理
可见，两电源共同作用的响应是两电源单独作用时响应之和。本例的结果证明了叠加定理的结论。
【例4-1-2】 应用叠加定理计算图4-1-4（a）所示电路中的电压u。并确定40Ω电阻消耗的功率。
解 本例若采用结点分析法，要建立两个结点方程，求解方程工作量不大，应该优先选择结点分析。用叠加定理分析时，独立电源分别作用的电路如图4-1-4（b）、（c）、（d）所示，三个电路的分析均可以采用分压、分流关系实现，计算工作量也不太大，可以选择叠加定理来分析。根据叠加定理，
。
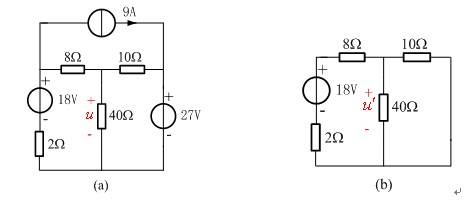
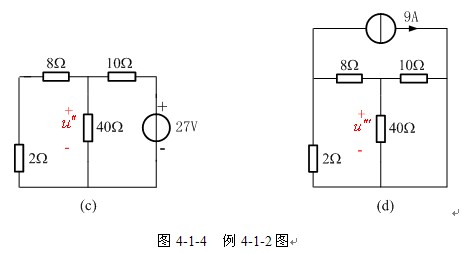
按照电阻串联、并联和分压关系，不难得到
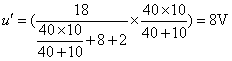
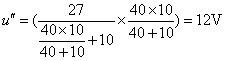
图（d）中， 10Ω和40Ω电阻并联，结果为8Ω电阻，两个8Ω电阻串联，再和2Ω并联，由分流关系不难得到
因此 
功率 
但
，即功率不符合叠加定理。
【例4-1-3】电路如图4-1-5（a）所示，试用叠加定理求受控电源端电压U及其提供的功率。
解 本例最简单分析方法应该是结点法，为了说明受控电源在叠加定理应用时的处理方法，在此用叠加定理分析。用叠加定理分析含受控电源电路时，受控电源保留在独立电源单独作用的各电路之中。电压源和电流源分别单独作用的电路如图4-1-5（b）和（c）所示。
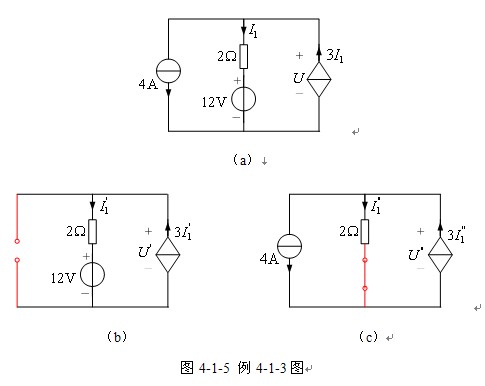
图4-1-5（b）中，由KCL和KVL分别得到
解得 
图 4-1-6（c）中，由KCL和KVL分别得到
解得 
当两电源共同作用时， 
受控电源提供的功率为 
【叠加定理应用注意事项】
1. 叠加定理仅适用于线性电路。
2. 应用叠加定理分析含受控源电路时，通常不把受控源单独作用于电路，而把受控源作为电阻元件一样对待，当某一独立电源单独作用时，受控源保留在电路中。
3. 叠加时应注意各响应分量的参考方向与原来的响应变量方向是否一致，方向一致则响应分量前应取“+”号，不一致则响应分量前应取“－”号。