1．数学上的傅里叶分解
满足狄里赫利条件的周期函数f(t)总可以分解为如下的傅里叶级数：
(8.1)
：
的角频率；T：f(t)的周期；A0、ak和bk：傅里叶系数。
A0是函数f(t)在一个周期内的平均值：
(8.2)
将它们代入式(8.1)即得到周期函数f(t)的傅里叶展开式。
2．傅里叶级数三角函数形式
设
、
代入式(8.1)。
其中
，
所以式(8.1)变换为
(8.8)
式中 
A0是常量，称为恒定分量或直流分量；
K=1时，
是正弦波，其频率与周期函数f(t)的频率相同，称为基波；
和
分别为基波的振幅和初相。
除恒定分量和基波外，其余各项统称为高次谐波。
3．频谱
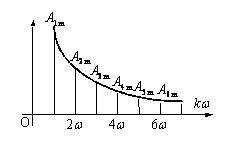
振幅频谱（如图）：
谐波振幅Amk随角频率
变动的情形用图形表示；Amk的量值，称为谱线，谱线间具有一定间隔的频谱称为离散频谱。
相位频谱：
各次谐波的初相
随角频率
变动的情形。
谐波分析：将周期函数分解为恒定分量和各次谐波方法。