一、汤逊理论
1.非自恃放电与自持放电
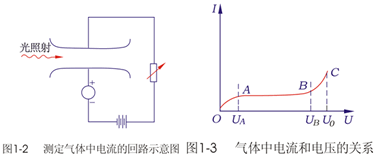
OA:电压![]() 电流
电流![]()
AB:稳定,外电离因素产里的带电质点分部落入电极,少隙和电流密度小,绝缘状态。
BC:新的电离——电子碰撞电离。
非自恃放电:外施电压小于Uo,间隙电流极小,取消外电离因素,电流消失。
自恃放电:Uo以后的放电,Uo后气体强烈电离,且电离过程可只靠电场作用自行维恃,不再需要光照等外电离因素。
C分界点,Uo击穿电压。
2.电子崩及电子电离系数
外电离因素使明极出现一个自由电子(光电效应),电场作用加建——碰撞电离——正离子;两自由电子,新的碰撞电离。
电子数20,21,22……2n雪崩增加。
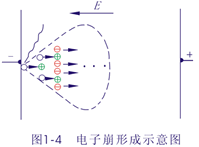
电子崩:因碰撞电离使自由电子数不断增加的想象。
电子崩过程——a过程,a碰撞电离系数
定义:一个电子沿电场方向行径1cm长度,平均发生的碰撞电离次数。曲路电流 I=Ioe2d I1=Ioe2d1 I2=Ioe2d2 I2-I1取对
图1-5单对数坐标,I-d直线,斜率![]()
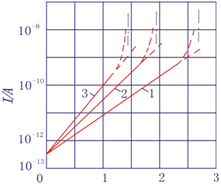
每次碰撞产生一个新电子,则a为单位行程内新电高出的电子数。
非自恃放电电流变化规律用电子碰撞电离过程解释。
分析a假设:
① 电子动能小于气体电离能,碰撞的产生电离。
② 电子动能大于气体电离能,碰撞产生电离。
③ 每次碰撞,不论是否造成电离,电子都失去全部动能,从0开始重新加速,两次碰撞间电子沿电场方风吹草动直线运动。
1cm内,140平均碰撞次数![]() ,行程x≥xi发生电离,碰撞电离条件
,行程x≥xi发生电离,碰撞电离条件![]() ≥Wi 即
≥Wi 即![]()
自由行程分布服从统计规律,关于xi概率,![]() 或记为
或记为![]()
则电离系数![]()
自由行程![]() ,空气相对密度
,空气相对密度![]()
Po.To标准参考大气条件下的气体压力和气体分子温度则![]() A常数
A常数![]() 的单变量函数
的单变量函数
![]() 又
又![]()
因此:![]() 令
令![]() 常数
常数
得![]()
![]() 反映每次碰撞平均产生的电子数,电离概率
反映每次碰撞平均产生的电子数,电离概率
![]() 反映电子在平均自由行程上由电场获得的能量
反映电子在平均自由行程上由电场获得的能量
![]() 过程——正离子引起电离
过程——正离子引起电离
3.![]() 过程与自恃放电条件
过程与自恃放电条件
![]() 过程:电极空间的碰撞电离
过程:电极空间的碰撞电离
![]() 过程:正离子及光子在阴极表面激发出电子,引起阴极表面电离
过程:正离子及光子在阴极表面激发出电子,引起阴极表面电离
阴极材料逸出功比气体分子电离能小得多,正负离子复合,分子由激励态跃迁回常态,产生光子,引起阴级表面电离
![]() :折算到每个碰撞阴极的正离子中在阴极释出的自由电子数。光电离阴极产生一个电子
:折算到每个碰撞阴极的正离子中在阴极释出的自由电子数。光电离阴极产生一个电子![]() 过程 阳极电子数
过程 阳极电子数![]() ,每次电离撞出一个正离子,电极空间
,每次电离撞出一个正离子,电极空间![]() 正离子,这些正离子到达阴极表面,撞出电子
正离子,这些正离子到达阴极表面,撞出电子![]() ,电子在电极空间碰撞产生,更多正离子循环。
,电子在电极空间碰撞产生,更多正离子循环。
阴极发射一个电子,阳极表面进入z个电子
![]() 级数收敛为
级数收敛为![]()
单位时间内阴极表面单位面积有![]() 个起始电子逸出,稳态后,单位时间进入阳极单位面积电子数
个起始电子逸出,稳态后,单位时间进入阳极单位面积电子数![]()
![]()
回路中电流![]()
![]()
![]() 过程使电流的增长指数规律还快
过程使电流的增长指数规律还快
d 小电场弱时,![]() 过程忽略不计
过程忽略不计
I、d实验曲线决定![]()
![]() 或
或![]() 不可能
不可能
实际上![]() 意味间隙被击穿,由外回路决定,不依赖外地离因素,由电压自动维持。
意味间隙被击穿,由外回路决定,不依赖外地离因素,由电压自动维持。
自持放电条件![]() 或
或![]()
物理解释:一个电子自己进入阳极后,![]() 、
、![]() 过程,在阴极上产生一个新的替身,天需外电离因素可继结下去。
过程,在阴极上产生一个新的替身,天需外电离因素可继结下去。
![]()
![]() 与材料逸出功相关
与材料逸出功相关
而且放电显然与电极材料及表面状态有关。
阴极表面 | 气体间隙中 | 阳极表面 | |
第1周期 | 一个电子逸出 | 形成 |
|
二、巴申定律与均匀电场击穿电压
1、巴申定律![]() 或
或![]() 击穿电压
击穿电压
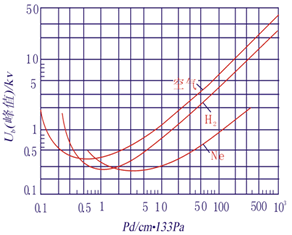
图1-7空气间隙的![]() 曲线,非单调函数,U形曲线,有极小值。
曲线,非单调函数,U形曲线,有极小值。
不同气体![]() 及对应的
及对应的![]() 不同
不同
![]() 极小值不出现在常态,而是出现在低气压,空气相对密度很小的情况下
极小值不出现在常态,而是出现在低气压,空气相对密度很小的情况下
2.均匀电场的击穿电压
![]() 代入自持放电条件
代入自持放电条件![]()
![]()
达至自持放电E=Eb击穿场强![]() 得
得![]()
![]() 由材料决定,但两次取对数,
由材料决定,但两次取对数,![]() 对Ub影响不了,常数,论以
对Ub影响不了,常数,论以![]() (1-22)
(1-22)
汤逊理论佐证巴申定律
巴申定律以实验结果支持汤逊定理。
(1-21)两边对![]() 求导,令导数为O
求导,令导数为O
![]()
![]()
理论,实验都说明Ub有极小值
U形曲线右半支,Ub随![]() 上升增加,
上升增加,![]() 电离减弱
电离减弱![]()
![]() 电子石易积累能量,电离
电子石易积累能量,电离![]()
左半支:![]() 主要是
主要是![]() ——电子平均行程
——电子平均行程![]() 个,积累的能量
个,积累的能量![]() 但空气密度低,分子数量少;机会少;电子追不到分子,撞进电极了。
但空气密度低,分子数量少;机会少;电子追不到分子,撞进电极了。
![]() 大
大 ![]() 小
小
高气压、高真空都可以提高击穿电压,工程上广泛使用。
会不会天限提高——不可能——声强高——强场发射,而且高能电子撞阳极,阳极表面气化。
另![]() 得
得![]()
![]() 小即
小即![]() 小,
小,![]() 电子来不及碰撞应进入阳极
电子来不及碰撞应进入阳极
![]() 大即
大即![]() 大,碰撞次数多
大,碰撞次数多
三、汤逊放电理论的适用范围
汤逊理论在坐低气压,![]() 较小的条件下在放电实验的基础上建立,
较小的条件下在放电实验的基础上建立,![]() 过小或过大,放电机理将变化,不再适用,
过小或过大,放电机理将变化,不再适用, ![]() 过小——气压极低(d不会过小)
过小——气压极低(d不会过小)![]() 小
小![]() 小即
小即![]() 大,
大,![]() 》d来不及碰撞电离,U 一定程度——场致发射导致击穿,碰撞电离理论不适用。
》d来不及碰撞电离,U 一定程度——场致发射导致击穿,碰撞电离理论不适用。
![]() 大——气压高,或d大,现象天使用汤逊理论解释
大——气压高,或d大,现象天使用汤逊理论解释
(1)放电外形:具有分支的细通道,汤逊理论,放电在全空间连续进行,辉光——电子崩
(2)放电时间:电子崩几个循队完成击穿,可计算时间,低气压计算符合实况,高压时,实测小于计算。
(3)击穿电压:![]() 小,Ub计算值与实验值一致,
小,Ub计算值与实验值一致,![]() 大不一致
大不一致
(4)阴极材料:低气压下击穿电压与材料、文气压下则无关。
![]() >0.26cm(pd>200cm.mmHg),汤逊理论计算结果不再适用。
>0.26cm(pd>200cm.mmHg),汤逊理论计算结果不再适用。
汤逊理论是将电流很小的滑流过程理论化,忽略了空间比荷的影响,d.![]() 较大时,不能忽略电子崩对电场的畸变。
较大时,不能忽略电子崩对电场的畸变。
