图1(a)所示是一个线性电感元件的交流电路。
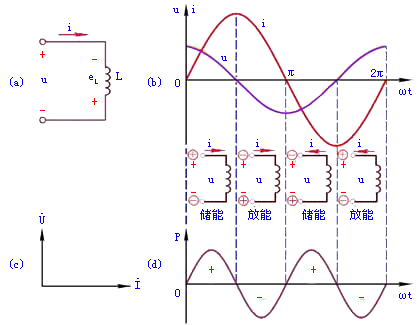 |
图1 电感元件的交流电路 (a) 电路图;(b) 电压与电流的正弦波形; (c) 电压与电流的相量图;(d) 功率波形 |
当电感线圈中通过交流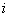 时,其中产生自感电动势
时,其中产生自感电动势 。设电流
。设电流 ,电动势
,电动势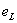 和电压
和电压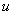 的参考方向如图1(a)所示。根据基尔霍夫电压定律得
的参考方向如图1(a)所示。根据基尔霍夫电压定律得
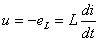
设电流为参考正弦量,即
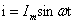
则
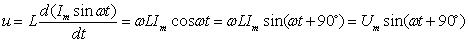 (1)
(1)
也是一个同频率的正弦量。
可见,在电感元件电路中,在相位上电流比电压滞后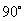 (相位差
(相位差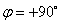 )。
)。
表示电压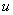 和电流
和电流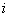 正弦波形如图1(b)所示。
正弦波形如图1(b)所示。
在式(1)中
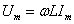
或
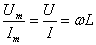 (2)
(2)
由此可知,在电感元件电路中,电压的幅值(或有效值)与电流的幅值(或有效值)之比值为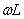 。显然,它的单位为欧[姆]。当电压
。显然,它的单位为欧[姆]。当电压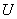 一定时,
一定时,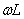 愈大,则电流
愈大,则电流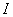 愈小。可见它具有对交流电流起阻碍作用的物理性质,所以称为感抗,用
愈小。可见它具有对交流电流起阻碍作用的物理性质,所以称为感抗,用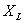 代表,即
代表,即
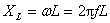 (3)
(3)
感抗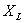 与电感
与电感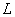 、频率
、频率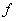 成正比。因此,电感线圈对高频电流的阻碍作用很大,而对直流则可视作短路,即对直流讲,
成正比。因此,电感线圈对高频电流的阻碍作用很大,而对直流则可视作短路,即对直流讲,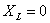 (注意,不是
(注意,不是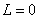 ,而是
,而是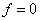 )。
)。
应该注意,感抗只是电压与电流的幅值或有效值之比,而不是它们的瞬时值之比,即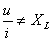 。因为这与上述电阻电路不一样。在这里电压与电流之间成导数的关系,而不是成正比关系。
。因为这与上述电阻电路不一样。在这里电压与电流之间成导数的关系,而不是成正比关系。
如用相量表示电压与电流的关系,则为
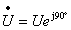
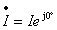
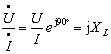
或
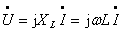 (4)
(4)
式(4)表示电压的有效值等于电流的有效值与感抗的乘积,在相位上电压比电流超前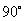 。因电流相量
。因电流相量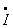 乘上j后,即向前(逆时针方向)旋转
乘上j后,即向前(逆时针方向)旋转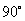 。电压和电流的相量图如图1(c)所示。
。电压和电流的相量图如图1(c)所示。
电感元件交流电路的瞬时功率为
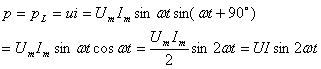 (5)
(5)
由上式可见,p是一个幅值为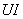 ,并以
,并以 的角频率随时间而变化的交变量,其变化波形如图1(d)所示。
的角频率随时间而变化的交变量,其变化波形如图1(d)所示。
在第一个和第三个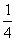 周期内,p是正的(
周期内,p是正的(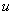 和
和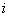 正负相同);在第二个和第四个
正负相同);在第二个和第四个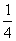 周期内,p是负的(
周期内,p是负的(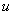 和
和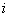 一正一负)。瞬时功率的正负可以这样来理解:当瞬时功率为正值时,电感元件处于受电状态,它从电源取用电能;当瞬时功率为负值时,电感元件处于供电状态,它把电能归还电源。
一正一负)。瞬时功率的正负可以这样来理解:当瞬时功率为正值时,电感元件处于受电状态,它从电源取用电能;当瞬时功率为负值时,电感元件处于供电状态,它把电能归还电源。
在电感元件电路中,平均功率
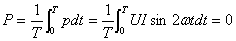
从上述可知,在电感元件的交流电路中,没有能[量]消耗,只有电源与电感元件间的能[量]互换。这种能[量]互换的规模,我们用无功功率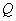 来衡量。我们规定无功功率等于瞬时功率
来衡量。我们规定无功功率等于瞬时功率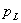 的幅值,即
的幅值,即
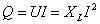 (6)
(6)
它并不等于单位时间内互换了多少能量。无功功率的单位是乏(var)或千乏(kvar)。
与无功功率相对应,平均功率也可称为有功功率。
例1、把一个0.1H的电感元件接到频率为50Hz,电压有效值为10V的正弦电源上,问电流是多少?如保持电压值不变,而电源频率改变为5000Hz,这时电流将为多少?
解:
当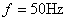 时
时
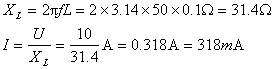
当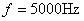 时
时
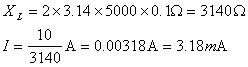
可见,在电压有效值一定时,频率愈高,则通过电感元件的电流有效值愈小。
