欲从卡诺图导出描述该函数的积之和表达式,则该表达式应占有卡诺图上全部函数值为1的小方格,而不能占有任何一个函数值为0的小方格。
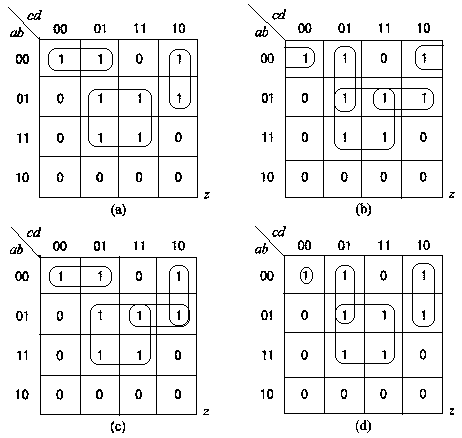
图 函数的卡诺图
上图给出了同一函数的4张卡诺图,由此写出下述(a),(b),(c)和(d)4个表达式:
(a) z = b d + a c d + a b c
(b) z = b d + a b c + a b d + a c d
(c) z = b d + a c d + a b c + a b c
(d) z = b d + a c d + a c d +a b c d
式(a)和(b)是无冗余表达式,式(a)为最简表达式。由卡诺图写积之和表达式时,希望该表达式不但是无冗余的,而且是最简的。为达到此目的,总力图用最少的卡诺圈把卡诺图中的填1小方格全部包含起来且尽可能使各卡诺圈包含尽可能多的填1小方格。从合并可能性最少的填1小方格开始画卡诺圈有助于得最简的表达式。
2.导出最简的和之积表达式
函数的和之积表达式,应占有卡诺图上的全部函数值为0的小方格而未占有任何一个函数值为 1 的小方格。用最少的卡诺圈把全部填0小方格包含起来,且尽可能把更多的填0小方格合并成最大的卡诺圈,可得最简表达式。从合并可能性最少的填0小方格开始伙卡诺圈,有助于得到最简的和之积表达式。
