逻辑函数和逻辑表达式

图1（a）

各输出变量和输入变量之间的关系可用含m个逻辑表达式的方程组

z_i=f_i(x₁,x₂,^...,x_n) i=1,2,^...,m (1)

式（1）是图1（a）所示组合电路的逻辑功能的数学描述。该组合电路则是实现这些逻辑函数的电气装置。

描述组合电路的逻辑函数称为组合逻辑函数。逻辑表达式是描述逻辑函数的一种代数形式。

1.导出逻辑表达式与真值表

数字电路应实现的逻辑功能通常是由某种文字描述给出的。如欲用数字电路实现这些功能，首先要把这一文字描述变换成一种可以进行逻辑变换的描述。真值表和逻辑表达式就是其种的两种描述方法。真值表具体地给出了自变量的全部取值组合下的函数值，所以，真值表是唯一的。对于有n个自变量的函数，其真值表有2ⁿ行。对于相同的逻辑功能可以由不同的逻辑表达式来描述。

2.积之和表达式与最小项表达式

设函数z的逻辑表达式为

z（a，b，c）=ab+ac (2)

a b和a c是由与（逻辑乘）运算连接的，称为与项（或乘积项，积项）。这两个与项又由或（逻辑

和）运算连接，所以，称这种类型的表达式为与--或表达式或积之和表达式。

式2真值表如下表所示

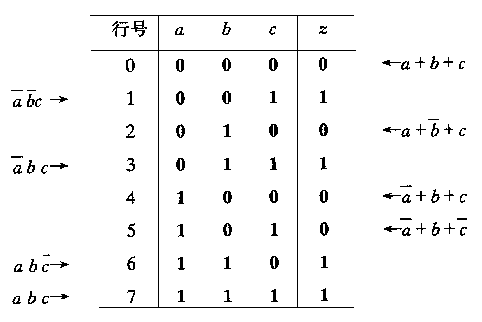
表2 真值表

z（a,b,c)= a b + a c

= a b(c + c) + a (b + a) c

= a b c + a b c + a b c + a b c（3）

上式也是积之和表达式。其真值表如表3所示。

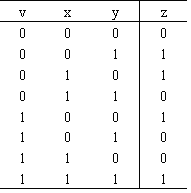
表3

最小项是一种特殊类型的乘积项。在一个n个自变量的逻辑函数中，包含全部n个变量的积项称为最小项,均由最小项构成的积之和表达式称为最小项表达式或标准的积之和表达式。

在式（3）中，各最小项的标号由下法求得：

最小项名a b ca b c a b c a b c

取值组合 1 1 11 1 00 1 1 0 0 1

标号 m₇m₆m₃m₁

从而式（3）可简写为

z(a,b,c)= m₁ + m₃ + m₆ + m₇

进而简作

z(a,b,c)=∑_m(1,3,6,7)

3.和之积表达式与最大项表达式

对式（2）进行变换，得

z(a,b,c)=(a + b)(a + c)(4)

上式可称为或-与表达式，或者和之积表达式。

对式（4）进行分解

z(a,b,c)=(a + b)(a + c)

=(a + b + c)(a + b + c)(a + b + c)(a + b + c)(5)

上式中的各和项仅使真值表中一行为0，故称它们为最大项，且称式（5）为最大项表达式或标准的和之积表达式。最大项是一种特殊的和项。在一个n变量的逻辑函数中，包含全部n个变量的和项称为最大项。最大项也常用标号表示。在式（5）中各最大项标号由下法求得：

最大项名(a + b + c)(a + b + c)(a + b + c)(a + b + c)

取值组合 0 0 0 0 1 01 0 0 1 0 1

标号 M₀ M₂ M₄M₅

从而式（5）可简写作

z(a,b,c)=M₀M₂M₄M₅=∏_M(0,2,4,5)=∏(0,2,4,5)

最小项和最大项具有如下性质：

a.所有最小项之和恒为1，即

∑m_i=1

b.任意两个最小项之积恒为0，即

m_i.m_j=0 i≠j

c.所有最大项之积恒为0，即

∏M_i=0

d.任意两个最大项之和恒为1，即

M_i+M_j=1 i≠j

e.标号相同的最大项和最小项互为反函数，即

m_i=M_j

f.任一含有n-k个变量的积（和）项均包含有2^k个最小（大）项。

如果已知函数的最小项表达式，则由未出现在该表达式中的各标号组成的最大项之积即为该函数的最大项表达式。反过来也是这样。

如果已知函数的最小项表达式，由相同标号组成的最大项表达式为该函数的反函数。反过来也是这样。