未完全规定的逻辑函数的化简

在许多实际问题中，由于具体条件的限制，某些取值组合下的函数值，可任意取0或1。这些取值组合称为无关项或约束项。这类函数称为未完全规定的逻辑函数或未完全描述的逻辑函数。

图1（a） 四舍五入电路

上图所示为四舍五入电路。该电路的输入为采用8421BCD码的1位十进制数

当（b₃b₂b₁b₀)_8421BCD>(4)₁₀时，z=1；否则，z=0。8421BCD码中，1010-1111为非法，这6个取值组合是不会出现的，所以可以不为它们规定电路的输出值。由此可以得到电路的真值表如表2及卡诺图如下图示：

表2 四舍五入电路真值表

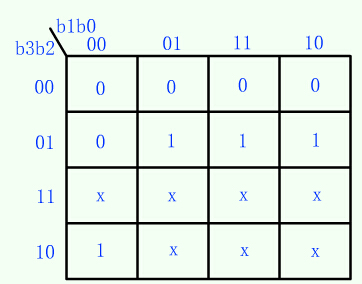
图2（b）真值表

由于1010这一取值组合是不会出现的，从而 b₃b₂b₁b₀=0， 同理

b₃b₂b₁b₀=0 b₃b₂b₁b₀=0 b₃b₂b₁b₀=0 b₃b₂b₁b₀=0 b₃b₂b₁b₀=0

进而 b₃b₂b₁b₀+b₃b₂b₁b₀+b₃b₂b₁b₀+b₃b₂b₁b₀+b₃b₂b₁b₀+b₃b₂b₁b₀=0

即 b₃b₁+b₃b₂=0

上式规定了不可能出现的各种取值组合，称为四舍五入电路的约束条件或约束方程。

2.未完全规定的逻辑函数的化简

由于未完全规定的逻辑函数的某些取值组合的函数值可取0或1，从而为简化该函数提供了更多的可能性。

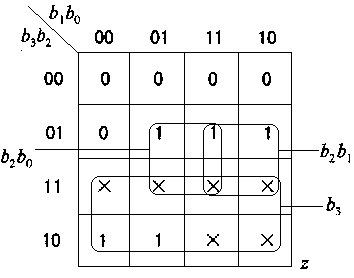
图2（b）给出了充分利用这一特性的一种卡诺圈的画法，它对应了最简的积之和表达式

z(b₃,b₂,b₁,b₀)=b₃+b₂b₁+b₂b₀

图3所示为对应的逻辑图。

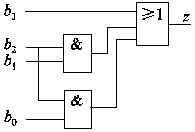
图3 四舍五入电路的逻辑图