1. 约束项、任意项和逻辑函数式中的无关项
在分析某些具体的逻辑函数时，经常会遇到这样一种情况，即输入变量的取值不是任意的。对输入变量取值所加的限制称为约束。同时，把这一组变量称为具有约束的一组变量。
例如，有三个逻辑变量A、B、C，它们分别表示一台电动机的正转、反转和停止的命令，A=1表示正转，B=1表示反转，C=1表示停止。因为电动机任何时候只能执行其中的一个命令，所以不允许两个以上的变量同时为1。ABC 的取值只可能是001、010、100当中的某一种，而不能是000、011、101、110、111 中的任何一种。因此，A、B、C 是一组具有约束的变量。通常用约束条件来描述约束的内容，为方便起见采用逻辑语言表述约束条件。
由于每一组输入变量的取值都使一个、而且仅有一个最小项的值为1，所以当限制某些输入变量的取值不能出现时，可以用它们对应的最小项等于0来表示。这样，上述例子中的约束条件可以表示为
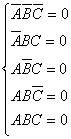
或写成 ： 
同时，把这些恒等于0的最小项叫做约束项。
有时还会遇到另外一种情况：在输入变量的某些取值下函数值是1还是0皆可，并不影响电路的功能。在这些变量取值下，其值等于1的那些最小项称为任意项。
由于约束项和任意项都不影响函数值，所以又把两者统称为逻辑函数式中的无关项，既可以写入函数式中，也可以不写进去。一般情况在用卡诺图表示逻辑函数时，首先将函数化为最小项之和的形式，然后在卡诺图中这些最小项对应的位置上填入1，其他位置上填入0。既然无关项可以包含也可以不包含在函数式中，那么在卡诺图中对应的位置上填1或0都可以。为此，规定在卡诺图中用×（或 
）表示无关项。在化简逻辑函数时既可以认为它是1，也可以认为它是0。