1. 表示最小项的卡诺图
将n变量的全部最小项各用一个小方块表示,并使具有逻辑相邻性的最小项在几何位置上也相邻的排列起来,所得到的图形叫做n变量最小项的卡诺图。因为这种表示方法是由美国工程师卡诺(Karnaugh)首先提出来的,所以把这种图形叫做卡诺图。下图画出了二到五变量最小项的卡诺图。
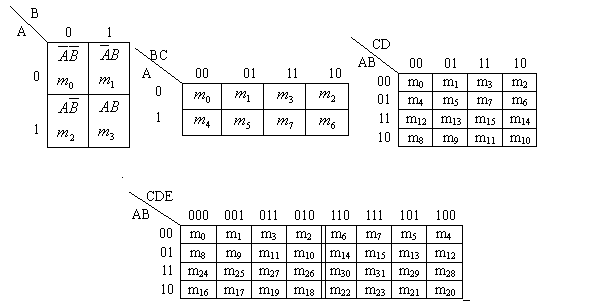
二到五变量最小项的卡诺图
图形两侧标注的0和1表示使对应小方格内的最小项为1的变量取值。同时,这些0和1组成的二进制数所对应的十进制数大小也就是对应的最小项的编号。
为了保证图中几何位置相邻的最小项在逻辑上也具有相邻性,这些数码不能按自然二进制数从小到达地顺序排列,而必须按图中的方式排列,以确保相邻的两个最小项仅有一个变量是不同的。
从二到五变量卡诺图上还可以看到,处在任何一行或一列两端的最小项也仅有一个变量不同,所以他们也具有逻辑相邻性。因此,从几何位置上应当把卡诺图看成是上下、左右闭合的图形。
在变量数大于等于5以后 ,仅仅用几何图形在两维空间的相邻性来表示逻辑相邻性已经不够了。如在五变量最小项的卡诺图中,除了几何位置相邻的最小项具有逻辑相邻性以外,以图中双竖线为轴左右对称位置上的两个最小项也具有逻辑相邻性。
2. 卡诺图表示逻辑函数
既然任何一个逻辑函数都能表示为若干最小项之和的形式,那么自然也就可以设法用卡诺图来表示任意一个逻辑函数。具体的方法是首先把逻辑函数化为最小项之和的形式,然后在卡诺图上与这些最小项对应的位置上填入1,在其余的位置上填入0,就得到了表示该逻辑函数的卡诺图。即任何一个逻辑函数都等于它的卡诺图中填入1的那些最小项之和。
例1:用卡诺图表示逻辑函数 ![]()
解:首先将Y化为最小项之和的形式
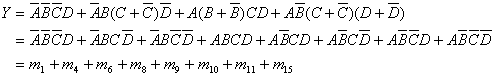
画出四变量最小项的卡诺图,在对应于函数式中各最小项的位置上填入1,其余位置上填入0,就得到如图所示的Y的卡诺图。
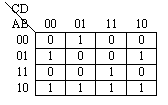
例2:已知逻辑函数的卡诺图如下,试写出该函数的逻辑式。
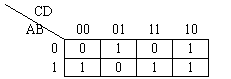
解:因为函数Y等于卡诺图中填入1的那些最小项之和,所以有
![]()
