一、 逻辑函数的最简形式
在进行逻辑运算时同一逻辑函数可以写成不同的逻辑式，而这些逻辑式的繁简程度又相差甚远。例如：
逻辑式越是简单，它所表示的逻辑关系越明显，同时也有利于用最少的电子器件实现这个函数。因此常常需要通过化简的手段找出逻辑函数的最简形式。表达式“繁——简”区分标准：
u 积之和式：和项越少越好，每个积项中变量个数越少越好
u 和之积式：积项越少越好，每个和项中变量个数越少越好
由于逻辑代数的基本公式和常用公式多以与——或形式给出，用于化简与——或逻辑函数比较方便，所以一般主要讨论与——或逻辑函数的化简。有了最简与——或逻辑函数后，再通过公式变换就可以得到其他类型的函数式了。究竟应该将函数式变换成什么形式，要视所用门电路的功能类型而定。但必须注意，将最简与——或式直接变换为其他形式逻辑式时，得到的结果不一定也是最简的。
二、常用的化简方法
代数（公式）化简法的原理就是反复使用逻辑代数的基本公式和常用公式消去函数式中多余的乘积项和多余的因子，以求得函数式得最简形式。公式化简法没有固定的步骤。现将经常使用的方法归纳如下。
1. 并项法
利用公式 
可以将两项合并为一项，并消去 
这一对因子。而且，根据代入定理可知, 
都可以是任何复杂的逻辑式。
例：
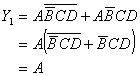
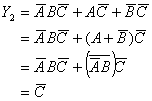
2. 吸收法
利用公式 
可将 
项消去。 
和 
同样也可以是任何一个复杂的逻辑式。
例：
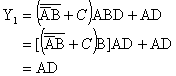
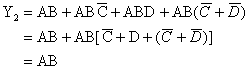
3. 消项法
利用公式 
及 
将 
或 
消去。其中A、B、C、D都可以是任何复杂的逻辑式。
例：
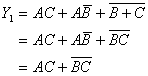
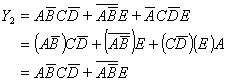
4. 消因子法
利用公式 
可将 
中的 
消去。 
均可以是任何复杂的逻辑式。
例：
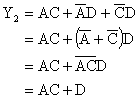
5. 配项法
u 根据基本公式中的 
可以在逻辑函数式中重复写入某一项，有可能获得更加简单的化简结果。
例： 
。
解：若在式中重复写入，则可得到
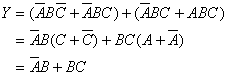
u 根据基本公式中的 
可以在逻辑函数式中的某一项上乘以 
，然后拆成两项分别于其他项合并，有时能得到更加简单的化简结果。
例： 
。
解：利用配项法可将Y写成
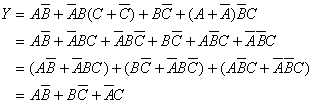
u 在化简复杂的逻辑函数时，往往需要灵活、交替地综合运用上述方法，才能得到最后的化简结果。
例： 
解： 
