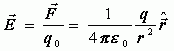存在于电荷周围的特殊物质叫电场。凡是有电荷的地方，周围就存在，即任何电荷都在自己的周围空间激发电场；而电场的基本性质是，它对处于其中的任何其它电荷都有力的作用，这个力叫电场力。
因此，电荷与电荷之间是通过电场相互作用的。
电场虽然不象原子、分子组成的实物那样看得见，摸得着，但近代物理的发展证明，它具有一系列物质的属性，如具有能量、动量，能施于电荷的作用力等等，因而能被我们所感觉。因此，电场是一种客观存在，是物质存在的一种形式。电场只是普遍存在的电磁场的一种形式。电磁场的物质性在它处于迅速变化的情况下才能更明显地表现出来，这个问题到了电动力学才进行详细的讨论。本章只讨论相对于观察者静止的电荷在其周围空间激发的电场，即静电场。
二、电场强度矢量
1、定义 
对于电场中任一固定点
，检验电荷
所受电场力与检验电荷的电量的比值
与无关，它反映了电场在点的性质。我们把它定义为电场强度矢量，简称场强，用
表示，即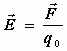
定义：电场任一点的电场强度是一矢量，其大小是单位电荷在该点所受电场力的大小，其方向与正电荷在该点所受的电场力的方向一致。
单位：牛顿/库仑（N/C)，伏特/米（V/m）。
如果电场中各点场强的大小和方向均相同，这样的电场称为均匀场，其场强矢量是相互平行的直线。
2、点电荷的场强 在  处有一点电荷 ，在 处放一检验电荷，点电荷 之间的相互作用力为
根据场强的定义, |
 |
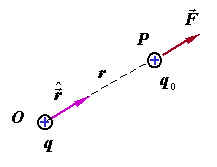当
时,点的场强沿矢径方向背离源点 ;当 
时, 点的场强 沿矢径方向指向源点。
三、场强叠加原理 
设空间有一组点电荷
，它们单独存在时对检验电荷 的电场力分别为
， 则
根据场强的定义，得
式中
分别代表 单独存在时所激发的电场在点的场强。
结论：一组点电荷所激发的电场在任一点的场强，等于各个点电荷单独存在时所激发的电场在该点场强的矢量和。这个结论叫电场强度矢量叠加原理，简称场强叠加原理。
四、场强的计算
1、点电荷和点电荷系的场强
点电荷 
点电荷系
例：求电偶极子的场强。
（1）连线延长线上点的场强
点电荷
和
存在时在 点产生的场强大小为
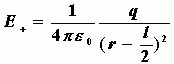(方向向右）
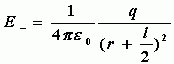（方向向左)
合场强的大小为
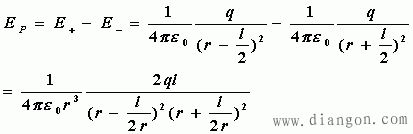
因为
，所以
(方向向右)
（2）中垂线上点的场强
点电荷和 存在时在点产生的场强大小为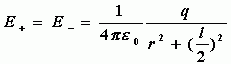
合场强的大小为
而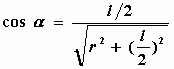
所以，合场强的大小为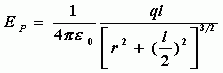
由于 ，那么
电偶极子的场强只与和
的乘积有关，这一乘积反映电偶极子的基本性质，它是一个描述电偶极子属性的物理量。我们将
定义为电偶极矩，其中
的方向是由指向。这样，电偶极子的场强公式可以写为:
在延长线上：
在中垂线上：
2、电荷连续分布带电体的场强
（1）电荷的体分布 
设有一电荷连续分布的带电体，电荷体密度为
,在带电体中取一体积元
，则该体积元中的体电荷元为
，它产生的场强为
由场强叠加原理，得整个带电体产生的场强为
（2）电荷的面分布 
设有一电荷连续分布的带电面，电荷面密度为
。在带电面中取一面积元
，则该面积元中的面电荷元为
，它产生的场强为
由场强叠加原理，得整个带电面产生的场强为
（3）电荷的线分布 
有一电荷连续分布的带电导线，电荷线密度为
,在带电导线中取一线段元
，则该线段元中的电荷元为 
，它产生的场强为
由场强叠加原理，得整根带电导线产生的场强为
