逻辑代数(布尔代数)：数学方法描述自然界和社会的各种因果关系(逻辑关系)的方法称为逻辑代数。
逻辑代数的特点：①变量取值只有0和1两个；②只有三种且基本运算：逻辑乘(与运算)、逻辑加(或运算)、逻辑否定(非运算或称求反)。
数字电路也称逻辑电路或开关电路。
(1)逻辑电平：数字电路中输入、输出信号大小均以逻辑值表示，电路某点电位高于某值(如2.4V)称为高电平“1”，低于某值(如0.4V)称为低电乎“0”。
(2)逻辑约定：两种逻辑约定。
正逻辑：约定高电平为“1”，低电平为“0”。
负逻辑：约定低电平为“1”，高电乎为“0”。
大多数系统中均采用正逻辑。
(3)正险冲与负脉冲：根据所用逻辑电路元件不同，数字电路中工作信号有正脉冲和负脉冲，这两种脉冲都可采用正逻辑或负逻辑约定。
2、基本逻辑运算及其实现——分立元件门电路(1)逻辑“与”(逻辑乘)：决定某事件(F)成立与否的诸条件(A，B，…)必须同时成立，该事件才能成立，这种逻辑关系称为逻辑“与”。可写成：F<<A B
实现“与”运算的最简电子电路称为与门。逻辑代数中输入变量(A，B，…)和输出变置(F)的取值只有0和1两个。将输人变量的不同取值组合与输出变量的关系列成表格称为逻辑状
态真值表。“与”逻辑关系可用口诀来助记：“有0出0，全1出1”。
(2)逻辑“或”(逻辑加)：决定某事件(F)成立与否的诸条件(A，B，…)中之一成立，该事件就成立，这种逻辑共系称为逻辑“或”。可写成：F<<A B C ……
实现“或”运算的电子电路称为或门，口诀是：“有1出1，全0出0”。
(3)逻辑“非”(逻辑否定)：当某条件A成立时，事件F产生与A相反的结果。可写成：F<</A
实现“非”运算的电子电路称为非门，口诀：“非0则l，非1则0”。
(4)复合逻辑运算：实现由上述三种基本逻辑运算组合而成的几种常用的复合运算关系的电路是市场供应的最基本逻辑器件。常见的复合逻辑门器件有与非门、或非门、异或门、与或非门等。
3、逻辑代数的基本定理和定律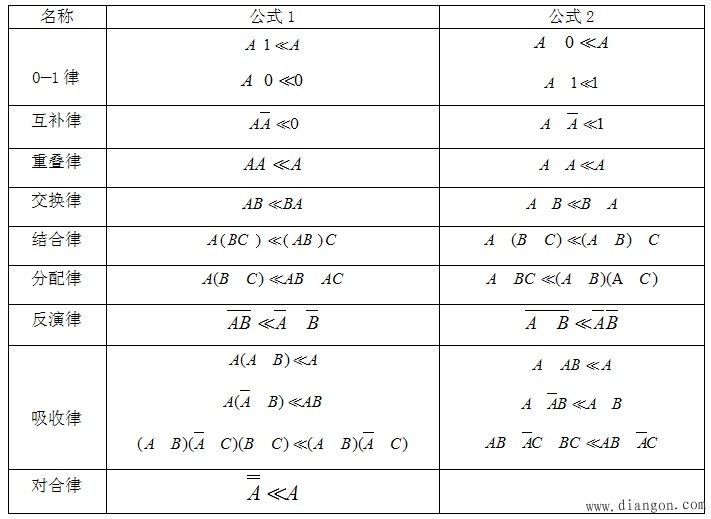
4、逻辑函数的表示方法
一个复杂的逻辑问题可用由与、或、非三种基本逻辑运算组合而成的逻辑函数来表达。其中输入条件是函数的自变量，其值取1称原变量，取0称反变量。如原变量为A，反变量为/A。输出逻辑结果为因变量，若因变量取1则称原函数，取0则称反函数。如原函数为F，反函数为/F。逻辑函数有4种表示方法：
(1)逻辑状态真值表：简称状态表或其值表。将全部自变量的所有取值组合与其相应的输出结果值列成一表，称为逻辑状态真值表。
一个自变量有两种取值(0和1)．两个自变量有4种取值组合(00，01，10，11)，3个自变最有8种取值组合，n个自变量有2n种取值组合。分析逻辑问题应先列出状态表，它保证了分析问题的全面性，因为逻辑状态表是唯一的。
(2)逻辑代数表达式：逻辑函数的代数表达式有原函数表达式和反函数表达式。前者因变量取1，后者则取0。从基本运算关系分．又有与或表达式和或与表达式，后者非本课程要求。
与或表达式是使因变量取1的各自变量取值组合的或运算(相加)．组合中各自变量(原变量或反变量)则进行与运算(相乘)。当表达式中的与项包含函数的全部自变量(原变量或反变置)，且每个自变量在该与项中只出现一次时，称为最小项。同一逻辑问题的逻辑函数表达式可写成多种形式，但只有全部用最小项组成的与或表达式是唯—的。如某三变量逻辑函数为
将各最小项代表的二进制取值组合用
，则函数可写成：
该表达式可由状态表直接列写出来。
(3)逻辑图：用逻辑符号表示的基本逻辑元件实现逻辑函数功能的电路图称为逻辑图。由于一个逻辑函数的表达式可以写成多种形式，因此同—个逻辑函数可以用不同的逻辑元件来实现，画出多种形式的逻辑电路图。
(4)卡诺图：将状态表中每一个变量取值组合(即每一个最小项)都用一个小方块表示，然后再将所有小方块按一定规则排列起来，就成为卡诺图。
(1)逻辑函数式的常见形式
一个逻辑函数的表达式不是唯一的，可以有多种形式，并且能互相转换。常见的逻辑式主要有5种形式，例如：
与—或表达式
或—与表达式
与非—与非表达式
或非—或非表达式
与—或非表达式
在上述多种表达式中，与—或表达式是逻辑函数的最基本表达形式。因此，在化简逻辑函数时，通常是将逻辑式化简成最简与—或表达式，然后再根据需要转换成其他形式。
(2)最简与—或表达式的标准
①与项最少，即表达式中“+”号最少。
②每个与项中的变量数最少，即表达式中“·”号最少。
(3)用代数法化简逻辑函数
用代数法化简逻辑函数，就是直接利用逻辑代数的基本公式和基本规则进行化简。代数法化简没有固定的步骤，常用的化简方法有以下几种。
①并项法。运用公式A +/A=1，将两项合并为一项，消去一个变量。如
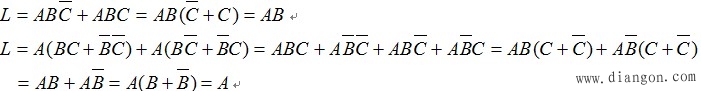
②吸收法。运用吸收律A+AB=A消去多余的与项。如
③消去法。运用
吸收律消去多余的因子。如
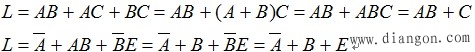
④配项法。先通过乘以A+ /A（=1）或加上A/A（=0），增加必要的乘积项，再用以上方法化简。如
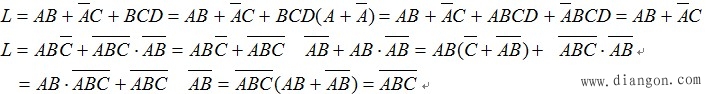
在化简逻辑函数时，要灵活运用上述方法，才能将逻辑函数化为最简。