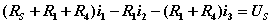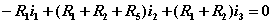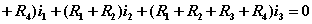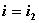回路电流法的基本思想

为减少未知量 ( 方程 ) 的个数，假想每个基本回路中有一个回路电流沿着构成该回路的各支路流动。各支路电流用回路电流的线性组合表示。来求得电路的解。
1. 回路电流法
　　以基本回路中的回路电流为未知量列写电路方程分析电路的方法。当取网孔电流为未知量时，称网孔法。 1）支路电流与回路电流的关系
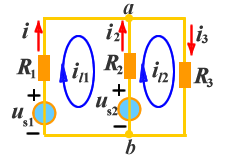　　上图所示电路有两个独立回路，选两个网孔为独立回路，设网孔电流沿顺时针方向流动，如图所示。可以清楚的看出，当某支路只属于某一回路（或网孔），那么该支路电流就等于该回路（网孔）电流，如果某支路属于两个回路（或网孔）所共有，则该支路电流就等于流经该支路两回路（网孔）电流的代数和。如上图电路中： 2）回路电流法列写的方程
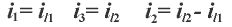　　回路电流在独立回路中是闭合的，对每个相关节点回路电流流进一次，必流出一次，所以回路电流自动满足KCL。因此回路电流法是对基本回路列写KVL方程，方程数为：b-(n-1)
　　与支路电流法相比，方程数减少n-1个。 　2.方程的列写
　　 应用回路法分析电路的关键是如何简便、正确地列写出以回路电流为变量的回路电压方程。以上图电路为例列写网孔的KVL方程，并从中归纳总结出简便列写回路KV方程的方法。
　　 按网孔列写 KVL 方程如下：

网孔1：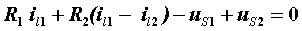
网孔2：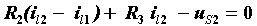

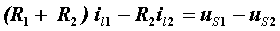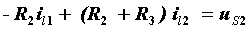　　将以上方程按未知量顺序排列整理得： 　　观察方程可以看出如下规律：
　　 第一个等式中，i_l1前的系数 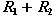是网孔1中所有电阻之和，称它为网孔1的自电阻，用R₁₁表示；i_l2前的系数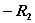是网孔1和网孔2公共支路上的电阻，称它为两个网孔的互电阻，用R₁₂表示，由于流过R₂的两个网孔电流方向相反，故R₂前为负号；等式右端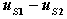表示网孔1中电压源的代数和，用u_S11表示，u_S11中各电压源的取号法则是，电压源的电压降落分向与回路电流方向一致的取负号，反之取正号。用同样的方法可以得出等式2中的自电阻、互电阻和等效电压源分别为：

自电阻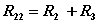

互电阻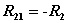

等效电压源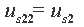

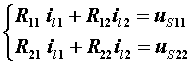
　　由此得回路（网孔）电流方程的标准形式：
　　　　　　
　　结论：对于具有l=b-(n -1) 个基本回路的电路，回路（网孔）电流方程的标准形式:
　　　　　　　
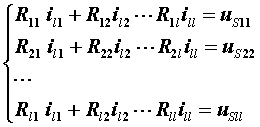
　　其中: 自电阻R_kk为正；
　　互电阻 R_jk＝R_kj可正可负，当流过互电阻的两个回路电流方向相同是为正，反之为负；
　　等效电压源u_Skk中的电压源电压方向与该回路电流方向一致时，取负号；反之取正号。
　　注：当电路不含受控源时，回路电流方程的系数矩阵为对称阵。
回路法的一般步骤：
　　(1) 选定l=b-(n -1)个基本回路，并确定其绕行方向；
　　(2) 对l个基本回路，以回路电流为未知量，列写 KVL 方程；
　　(3) 求解上述方程，得到l个回路电流；
　　(4) 求各支路电流(用回路电流表示 ) ；
　　(5) 其它分析。
注：电路中含有理想电流源和受控源时，回路方程的列写参见例题。 例题 列写如下电路的回路电流方程，说明如何求解电流 i. 　解1：

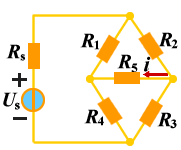独立回路有三个。选网孔为独立回路如图所示，回路方程为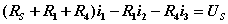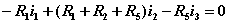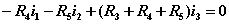： 　　从以上方程中解出网孔电流1和网孔电流2，则电流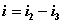
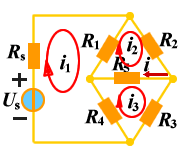	选网孔为独立回路

　　注：本题结果说明：
　　(1)不含受控源的线性网络，回路方程的系数矩阵为对称阵，满足 R_jk = R_kj。
　　(2)当网孔电流均取顺时针或逆时针方向时，R_jk均为负。

　解2：

为了减少计算量，可以只让一个回路电流经过R5支路如图所示。此时回路方程为： 　　从以上方程中解出网孔电流2，则电流
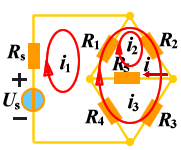	一个回路电流经过R5支路

　　注：解法2的特点是计算量减少了，但互有电阻的识别难度加大，易遗漏互有电阻。本题也说明独立回路的选取有多种方式，如何选取要根据所求解的问题具体分析。