1. “与”逻辑关系及运算
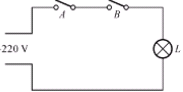
决定结果成立的所有条件都具备时，结果才成立，这种条件与结果之间的关系称为“与”逻辑。
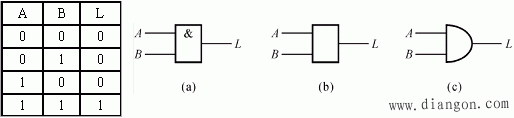
以二只串联开关控制一只电灯为例，只有当二只开关都闭合时，电灯才亮。令开关闭合和灯亮为逻辑“1”，开关断开和灯暗为逻辑“0”时，有如表所示的真值表。
该“与”逻辑关系也可写成逻辑表达式形式：
。
从逻辑运算上，是逻辑乘关系，0×0=0，0 ×1=0，1 ×0=0，1 ×1=1，“与”逻辑关系用“与”门逻辑符号表示：
2. “或”逻辑关系及运算
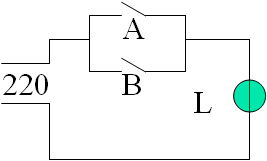
决定结果成立的所有条件只要有一个具备时，结果就成立，这种条件与结果之间的关系称为“或”逻辑。这种关系在日常生活中也是非常普遍的。以二只并联开关控制一只电灯为例，当其中一只开关闭合时，电灯就亮。 令开关闭合和灯亮为逻辑“1”，开关断开和灯暗为逻辑“0”时，有如表所示的真值表。
逻辑关系式为：
。
逻辑运算为逻辑加0+0=0，0+1=1，1+0=1，1+1=1，逻辑符号如下：
真值表：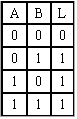
3. “非”逻辑关系及运算
条件具备时，结果不成立，条件不具备时结果成立，这种条件与结果之间的关系称为“非”逻辑。逻辑式为：
，是求反运算。
逻辑符号如下：
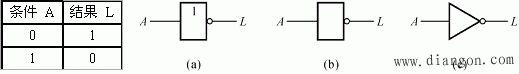
4.复杂和复合逻辑关系
(1) 异或逻辑关系
二个条件相同时，结果不成立，二个条件相异时，结果成立。 函数式：
。
逻辑符号：
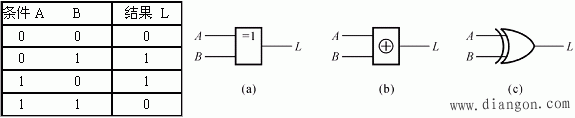
(2) 同或逻辑关系
二个条件相同时，结果成立，二个条件相异时，结果不成立。 函数式：
。
逻辑符号：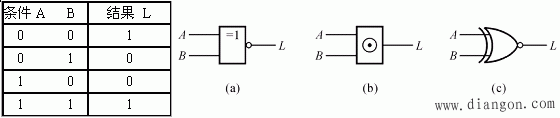
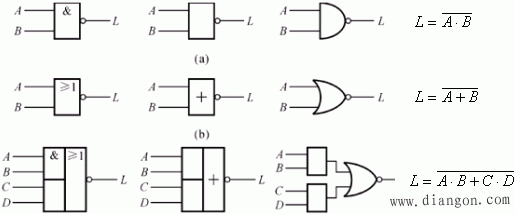
(3)复合逻辑关系
它由“与”、“或”、“非”三种基本逻辑关系组合而成。
二、逻辑运算中的运算定律，常用公式，运算规则
逻辑运算中只有逻辑加、逻辑乘和求反三种运算。
1 . 运算定律
0-1律：
重叠律：
互补律：
否定之否定律：
交换律：
结合律：
分配律：
荻魔根定律：
，其中后四个定律可以用前四个进行证明成立，也可用真值表证明等式成立。
2 .常用公式
，
，
，
，
，
3 .运算规则
对偶规则：“0” →“1”、“1” →“0”、“
” →“+”、“+” →“”变换前后两式为对偶式，并成立。
反演规则： “0” →“1”、“1” →“0”、“” →“+”、“+” →“”、原变量换反变量、反变量换原变量，变换后的式子是原函数的反函数。
三、逻辑函数的表示方法及标准表达式
1 . 逻辑问题的五种表示方法
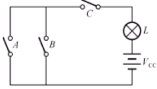
下图是三只开关控制一只电灯电路。
(1) 真值表表示
令开关合上为“1”，不合为“0”，灯亮为“1”，暗为“0”时真值表。
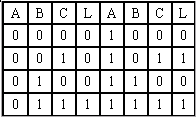
(2) 函数表达式表示：
。
(3)逻辑图和波形图表示：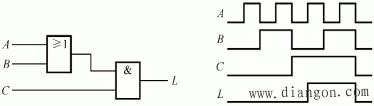
2 . 逻辑函数的标准“与—或”表达式
三开关控制一只电灯的逻辑问题的三种表达式：
第一种是由各“与项”之和组成，而每个“与”项是一个最小项，即是标准“与—或”表达式。
最小项：最小项中的变量个数和函数中的变量数相同，但最小项中的变量可以是函数的原变量，也可以是反变量。因此，上述例子的标准“与—或”表达式应该是：
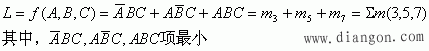
因此,变量的逻辑函数，应有8个最小项(
)。
由此可见:对输入变量的任何一种取值，只有一个最小项的值为1；任何二个最小项相与结果为零(即
)；全部最小项之和，其值恒为1(即
)；只差一个变量不同的二个最小项，逻辑上称相邻，可合并成一项，并消去一个变量。只差一个变量不同的二个最小项，逻辑上称相邻，可合并成一项，并消去一个变量。
3. 逻辑函数的标准“或—与”表达式
“或—与”表达式由各“或”项之积组成，而每个“或”项是一个最大项。
最大项：最大项中的变量个数和函数中的变量数相同，最大项中的变量同样可以是原变量，也可以是反变量。因此，三只开关控制电灯例子的标准“或—与”表达式应该是：
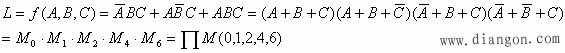
与最小项时对应，最大项对输入变量的任何一种取值，只有一个最大项的值为0；任何二个最大项相或，结果为1，即：
。全部最大项之积，其值恒为0，即：
。
只差一个变量不同的二个最大项，逻辑上称相邻，可合并成一项，并消去一个变量。
上述可见：最小项之和和最大项之积式只是同一个逻辑问题的二种不同表示方法。是一种互补的表示方法，有：
。