逻辑函数的化简就是使一个最初的逻辑函数经过化简后得到式中的“与”项，“或”项项数最少，而每项中的变量数也最少。从而使组成的逻辑电路最简(逻辑门数和每门的输入端数最少)。
二、逻辑函数的代数法化简
代数法是利用逻辑代数工具来达到使式子简化的目的。化简依据：逻辑代数定律、常用公式、和运算规则进行化简。常用方法：有吸收法、配项法、合并法、消去法、 冗余法等。代数法化简虽然简单，但必须熟悉逻辑代数运算规则等，且具有一定的试探性，否则达不到最简的目的。
三、逻辑函数的卡诺图法化简
1. 卡诺图：用方格图来描述逻辑函数，由于该方法由卡诺首先提出，所以把方格图称为卡诺图。
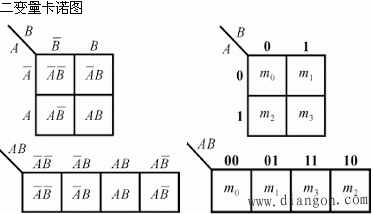
2. 如何画卡诺图：n个变量的函数，就有
个小方格，一个小方格对应一个最小项，下面是2～5变量卡诺图。
(a) 二变量A、B卡诺图：
，
。
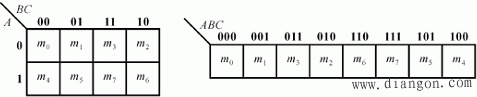
(b) 三变量A、B、C卡诺图
三变量的八个最小项：
。8个最小项在卡诺图小方格上的位置必须以相邻放置→相邻方格中的最小项只差一个变量不同，其他相同。
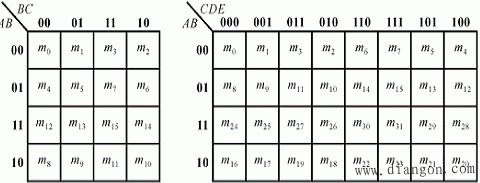
(c) 四变量卡诺图和五变量卡诺图
3. 逻辑函数的卡诺图表示
方法：首先将函数化成标准的“与—或”式，(最小项之和表达式)，将式中最小项相应的小方格填“1”，式中没有的最小项代表的小方格填“0”。填写好后的图形就是该函数的卡诺图了。
4. 卡诺图化简的依据
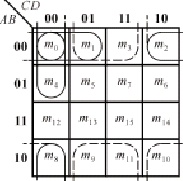利用了相邻二个小方格代表的最小项只差一个变量的相邻性,它们可以合并成一项,消去一个变量的性质进行。下面用四变量卡诺图为例加以说明。
如：m0与m1结合(画包围圈)，即：
。
m0与m4结合(画包围圈)，即：
。
m1与m3结合(画包围圈)，即：
。
m0与m2结合(画包围圈)，即：
。
m1、m3、m9、m11结合，即：
。
m0、m2、m8、m10结合，即：
。
结论：包围小方格结合最小项时，其结果是：消去包围圈中不同的变量，保留相同的变量。
卡诺图化简时的一般原则和规律：
1. 只能对个相邻方格实施包围，包围圈越大，式子越简；
.2 . 小方格可以重复包围，但每一包围必须含有一个未被包围过的方格，否则多余；
3. 包围“1”格得原函数，包围“0”格得反函数，经二次求反后分别可用“与非”逻辑和“或非”逻辑实现。
四、具有约束条件的逻辑函数的化简
1.什么样的逻辑函数称为具有约束的逻辑函数?
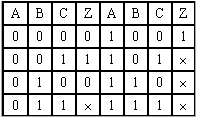在许多逻辑问题中，逻辑变量与逻辑结果之间存在着某种限制、制约和约束的关系，如十字路口交通信号控制灯和汽车通行之间的关系。在任何时间，红、绿、黄三只灯中只允许有一只灯亮，而不允许同时有二只或以上的灯亮，来控制指挥汽车通行、停止和准备。令灯暗为“0”，亮为“1”，车停为“1”，行为“0”。“×”为不允许出现(受制约的)灯亮组合，则有如下真值表。A－红，B－绿，C－黄时真值表：从表看出：输入变量的
组合是不允许出现的，是制约关系，这些项的取值与函数的结果无关。所以，这些项称为无关项、约束项，或是任意项等。
2.具有约束条件的逻辑函数的表示方法
具有约束条件的逻辑函数，用最小项和约束项一起表示出来。
约束条件：
或
。
3.如何简化具有约束的逻辑函数
由于约束项的存在与函数的结果无关，因此，在化简时，约束项的取值可以当作“1”，也可以当作“0”处理，在卡诺图中用符号“×”表示，以表示和其它最小项区别。