1.十进制数
在表示物理量的大小时,一般使用进位计数制。十进制(Decimal System)是最常用的进位数制,它采用了0、1、2、3、4、5、6、7、8、9十个计数符号,这些计数符号称作数码,数码的个数叫做基数。进位计数制是把数码按一定规律排列起来表示数的。具体地说,在计数过程中,当某一位累计到基数时,便向高位进一,而本位又从零开始计数。十进制的基数为10,所以十进制的计算规则是“逢十进一”。因此,在进位计数过程中,当数码处于不同位置时,所表示的数值大小是不同的。例如,十进制数165.8可以展开为
![]()
一个十进制数 N可以表示成:![]()
式中,Ki为基数“10”的第i次幂的系数,![]()
2.二进制数
若在数字电路中采用十进制,在电路实现上必须要有十个状态与十个数码相对应。在技术上有许多困难,而且很不经济。 二进制在电路上却很容易实现,所以就自然成为数字电路中最常用的进位计数制。
二进制数采用0和1两个数码,其基数是2,计数时“逢二进一”。例如:![]()
一个二进制数 N可以表示成: ![]()
式中,Ki为基数2的第i次幂的系数,![]()
可以看出,二进制数与十进制数的区别在于数码的个数和进位的规律不同。一个二进制数可以转换为与其等效的十进制数,转换时只要把每一位的等值十进制数相加就可以了。例如,将二进制数1011.01转换为十进制数:
![]()
3.十六进制数
为了克服二进制位数多、不便于书写和记忆的缺憾,在数字电路中还常采用 十六进制。十六进制采用0~9和A、B、C、D、E、F十六个数码,其中A~F分别对应于十进制数的10~15。十六进制的基数是16,计数时“逢十六进一”。例如:
![]()
一个十六进制数N可表达如下:![]()
式中Ki为基数16的第i次幂的系数,![]()
将十六进制数中每一位的等值十进制数相加,就可得到等效的十进制数。如:
![]()
由于四位二进制数正好等于一位十六进制数,因此,二进制数与十六进制数可以很方便地相互转换。将二进制数转换成十六进制数时,以小数点为界,沿前后两个方向把四位二进制数划为一组,把每一组用等值十六进制数代替,便得到等值十六进制数。例如:
![]()
反之,将十六进制数转换为二进制数时,只要将十六进制数逐位用相应的四位二进制数代替即可。例如:
![]()
由此可见,同一个数,用十六进制记数要比用二进制记数方便得多,再加上二进制与十六进制之间的转换很容易,因此,在数字系统中也经常用十六进制记数。
4.十进制数转换成二进制数
前面已经介绍过如何将二进制和十六进制数转换成十进制数,也介绍了二进制与十六进制之间的转换。现在介绍如何把十进制数转换成二进制数。
将十进制数转换成二进制数,要对整数部分和小数部分分别进行。整数部分的转换方法可以概括为“除二取余,余数倒排”;小数部分的转换方法可以概括为“乘2取整,整数顺排”。例如,将十进制数(25)D转换为二进制数。

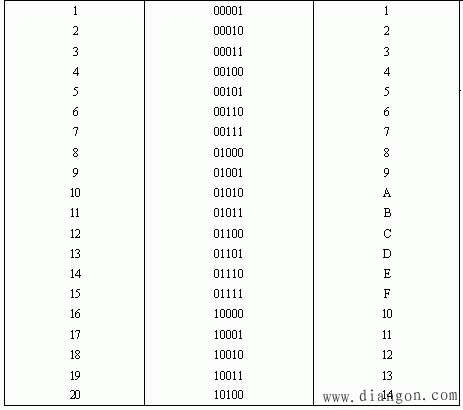
至于十进制数转换成十六进制数,可先将十进制数转换成二进制数,再将二进制数转换成十六进制数。为便于对照,将十进制、二进制和十六进制之间的关系列于表1中。
表1 几种数制之间得关系对照表