不同数制只不过是按一定规律对数进行描述的不同形式。同一个数可以用不同的进位制表示,即它们可以相互转换。数制转换有两种基本方法,一种是多项式替代法,另一种是基数乘除法。其次,对于某些特殊进位制之间的转换,可以采用按位分组进行。
1.多项式替代法
该法通常用于将一个任意进制数转换成十进制数。采用多项式替代法将一个R进制数转换成十进制数时,只需将R进制数按权展开,求出各位数值之和,即可得到相应十进制数。
例如,将二进制数10110. 011转换成十进制数:
(10110.011)2=1×24+1×22+1×21+1×2-2+1×2-3
=16+4+2+0.25+0.125
=(22.375)10
即 (10110.101)2=(22375)10
2.基数乘除法
该法用于将一个十进制数转换成任意进制数。采用基数乘除法将一个既包含整数部分,又包含小数部分的十进制数转换成R进制数时,应对整数部分和小数部分分别处理。整数 部分转换的方法是“除R取余,逆序排列”法,即将十进制整数反复除R,依次列出余数,先得到的余数是相应R进制整数的低位,后得到的余数是相应R进制整数的高位;小数部分转换的方法是“乘R取整,顺序排列” 法,即将十进制小数反复乘R,依次列出所得整数,先得到的是相应R进制小数的高位,后得到的是相应R进制小数的低位。
例如,将十进制数35.625转换成二进制数:
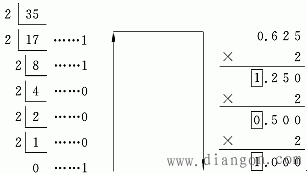
即 (35.625)10=(100011.101)2
