图1所示是一RL串联电路，也可分三种响应对其进行暂态分析。
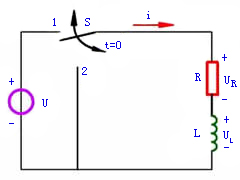
在图1中，如果在t=0时将开关S合到位置1上，电路即与一恒定电压为U的电压源接通，其中电流为i。
根据基尔霍夫电压定律，列出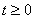
时的电路的微分方程
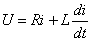
当初始值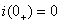
时，经求解可得
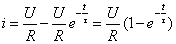(1)
这是RL电路的零状态响应。
 |
|
图1 RL电路 |
上式中
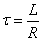
它也具有时间的量纲，是RL电路的时间常数。
如果在图1中，当电流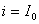
[即初始值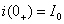
]时，即将开关S从位置1合到位置2，脱离电源，电流开始衰减，稳态值
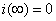，则
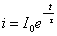(2)
这是RL电路的零输入响应。
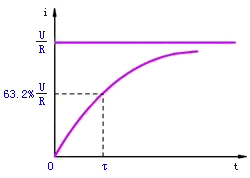
式(1)和式(2)的i随时间的变化曲线分别如图2和图3所示。
零状态响应与零输入响应两者叠加，即得RL电路的全响应
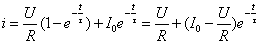(3)
式中：稳态值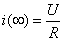
；初始值
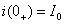；时间常数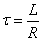
。这与三要素法的一般式(1)也是相当的。
 |
 |
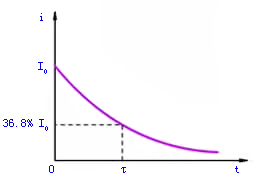| 图2 零状态响应 | 图3 零输入相应 |
由式(1)和式(2)可分别求出零状态响应和零输入响应时：
 |
|
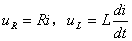
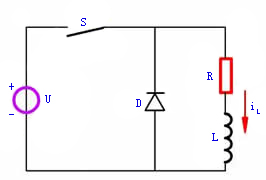
图4 例1的图 |
例1、在图4中，RL是一线圈，和它并联一二极管D。设二极管的正向电阻为零，反向电阻为无穷大。试问二极管在此起何作用？
解：在正常工作开关S闭合时，电流只通过线圈。当S断开时，由于线圈中产生自感电动势，它维持电流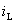
经二极管D在原方向流动而逐渐衰减为零。在此，二极管起续流作用。
如无二极管与线圈并联，当将S断开时，线圈中产生很高的自感电动势，它可能将开关两触头之间的空气击穿而造成电弧以延缓电流的中断，开关触头因而被烧坏。此外，很高的电动势对线圈的绝缘和人身安全也都是不利的。并联上二极管后，线圈两端电压接近于零，起保护作用。