图(a)所示为一个含线性电阻、电感和电容等元件,但不含独立源的一端口N0。
当它在角频率为ω的正弦电压(或正弦电流)激励下处于稳定状态时,端口的电流(或电压)将是同频率的正弦量。
应用相量法,端口的电压相量与电流相量的比值定义为该一端口的阻抗 Z(又叫等效阻抗,输入阻抗,驱动点阻抗)。
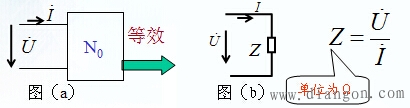
1.Z 和总电流、总电压的关系
由复数形式的欧姆定律![]()
可得:
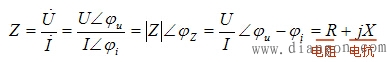
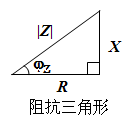
阻抗模:![]() 阻抗角:
阻抗角:![]()
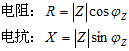
![]()
阻抗适合于串联电路的计算,单位是欧姆。
2.单一元件的复阻抗
正弦激励下
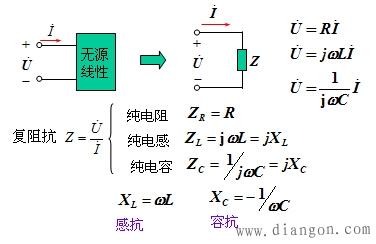
3.Z和电路性质的关系(以RLC串联电路为例)

当信号角频率一定时,电路性质由参数决定
ω L > 1/ω C ,X>0, φZ>0,电压领先电流,电路呈感性;
ω L<1/ω C ,X<0, φZ <0,电压落后电流,电路呈容性;
ω L=1/ω C ,X=0, φZ =0,电压与电流同相,电路呈电阻性。
问题讨论:
对RLC串联电路,假设R、L、C已定,电路性质能否确定?(阻性?感性?容性?)
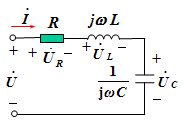
不能!
∵![]()
当ω不同时,可能出现:
XL > XC ,或 XL < XC , 或 XL =XC 。
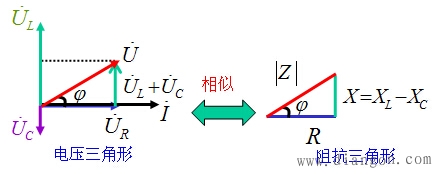
4.阻抗三角形和电压三角形的关系
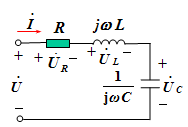
![]()
![]()