逻辑函数的简化
函数的简化依据:
1.逻辑电路所用门的数量少
2.每个门的输入端个数少
-->降低成本
3.逻辑电路构成级数少
4.逻辑电路保证能可靠地工作
-->提高电路的工作速度和可靠性
代数法化简函数
与或表达式的简化
1. 首先是式中乘积项最少
实现电路的与门少
下级或门输入端个数少
2.乘积项中含的变量少
与门的输入端个数少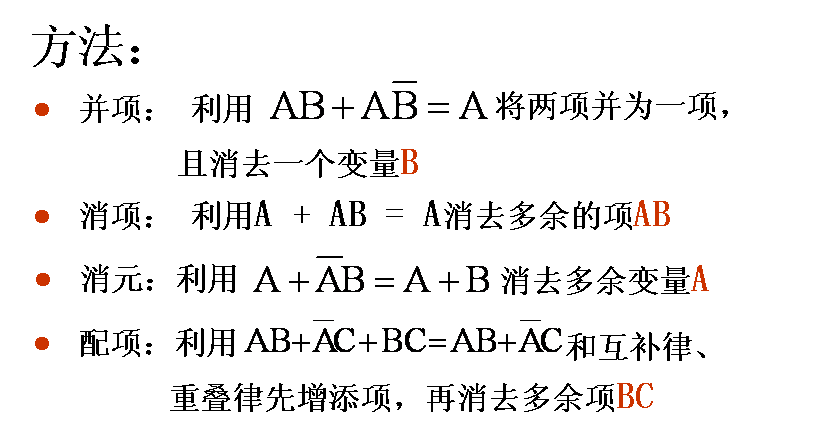
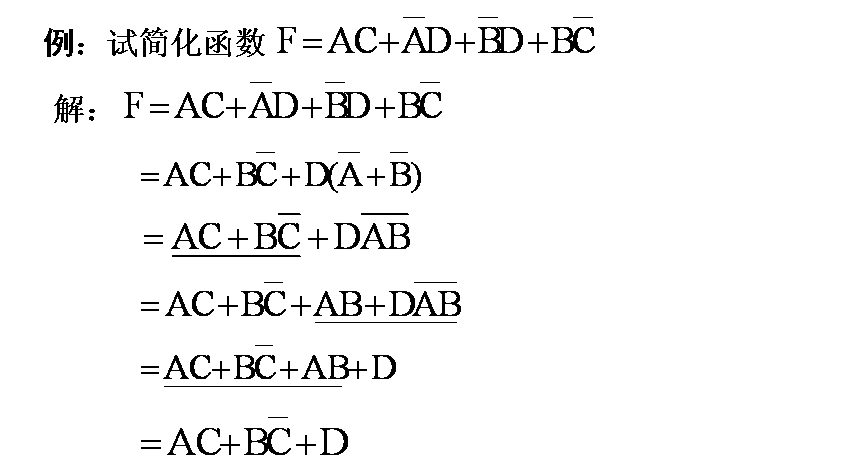
或与表达式的简化
F(或与式)求对偶式 F`(与或式)简化 F`(最简与或式)求对偶式 F(最简或与式)
卡诺图(K图)
图中的一小格对应真值表中的一行,即对应一个最小项,又称真值图
K图的特点:
1. k图为方形图。n个变量的函数--k图有2n个小方格,分别对应2n个最小项;
2. k图中行、列两组变量取值按循环码规律排列,使变量各最小项之间具有逻辑相邻性(上下左右几何相邻的方格内,只有一个因子不同)。
3. 有三种几何相邻:邻接、相对(行列两端)和对称(图中以0、1分割线为对称轴)方格均属相邻.
卡诺图化简函数规则:
几何相邻的2i(i = 1、2、3…n)个小格可合并在一起构成正方形或矩形圈,消去i个变量,而用含(n - i)个变量的积项标注该圈。
步骤:
1.先将函数填入相应的卡诺图中,存在的最小项对应的方格填1,其它填0。
2.合并:按作圈原则将图上填1的方格圈起来,要求圈的数量少、范围大,圈可重复包围但每个圈内必须有新的最小项。
3.每个圈写出一个乘积项。按取同去异原则
4.最后将全部积项逻辑加即得最简与或表达式
根据函数填写卡诺图
1、已知函数为最小项表达式,存在的最小项对应的格填1,其余格均填0。
2、若已知函数的真值表,将真值表中使函数值为1的那些最小项对应的方格填1,其余格均填0。
3、函数为一个复杂的运算式,则先将其变成与或式,再用直接法填写。
作圈的步骤
1、孤立的单格单独画圈
2、圈的数量少、范围大,圈可重复包围但每个圈内必须有新的最小项
3、含1的格都应被圈入,以防止遗漏积项
例1:直接给出函数的真值表求函数的最简与或式。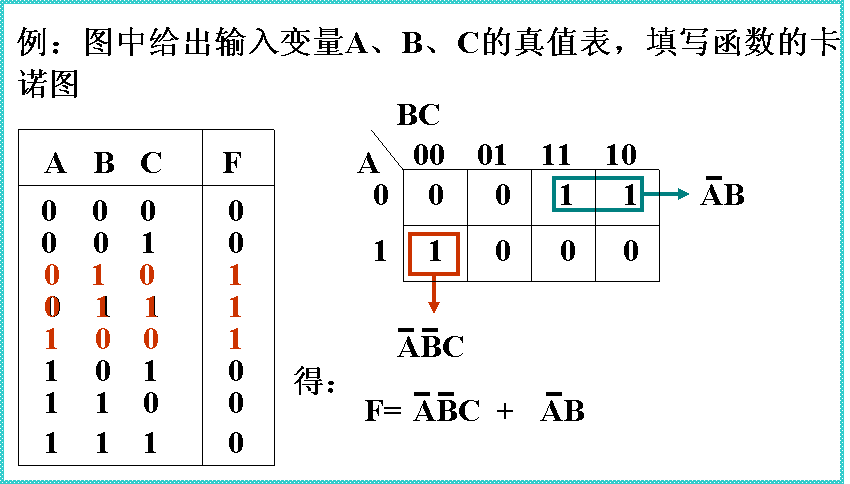
例2:直接给出函数的复杂的运算式。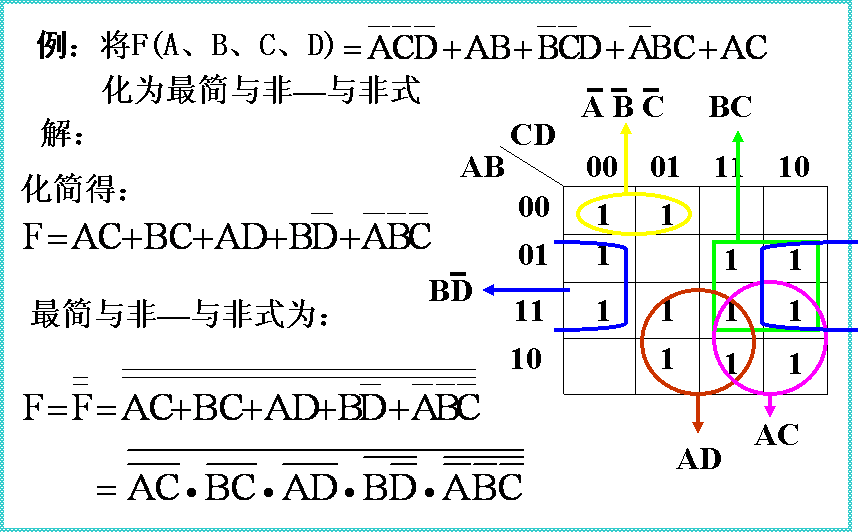
例4:含有无关项的函数的化简。
含有无关项的函数的化简:
无关项 对于变量的某些取值组合,所对应的函数值是不定。通常约束项和任意项在逻辑函数中统称为无关项
处理方法:
1.填函数的卡诺图时只在无关项对应的格内填任意符号“Φ”、“d”或“×”。
2.化简时可根据需要视为“1”也可视为“0”,使函数化到最简。
逻辑函数简化中的几个实际问题
1. 具有多输出端电路的简化
2. 只允许原变量输入的逻辑电路的简化
