相量分析法
相量分析法是针对正弦量激励下、且电路已进入稳态时的动态电路的分析。因为电路在正弦量的激励下，各处的响应都是同频率的正弦量，因此，将电路的激励和响应都用相量来表示，把电阻、电感、电容元件用复数阻抗或复数导纳表示，将电路定律用相量形式表示，把时域电路转换成相量电路之后，描述动态电路的方程就由时域中的微分方程转换为频域中的复数代数方程，求解复数代数方程，求得各响应的相量，然后再将这些响应的相量转换成时域的正弦函数表达式。
相量分析法的步骤
正弦量用相量表示，电阻、电感、电容元件用阻抗或导纳表示，画出相量电路；
2 、相量电路中，用电阻电路的分析方法求解各响应的相量；
3 、将求得的响应相量转换成时域的正弦函数表达式。
例 7.4-1 电路如图 7.4-1 （ a ）所示，已知 
，求 uS ， iL 和 ic 。
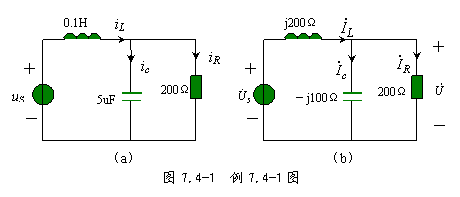
解：电流 iR 的相量为
感抗
容抗
所以，得到相量电路如图 7.4-1 （ b ）所示。
图 7.4-1 （ b ）中，有
则
由 KCL 得
由 KVL 得
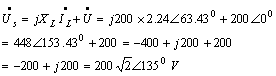
将相量再转换成正弦函数表达式，得
例 7.4-2 电路如图 7.4-2 所示，已知 
， 
，电压源的角频率 
，求电流 i1 和 i2 。
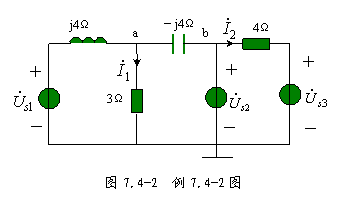
解：用节点电压法求解，设节点 a 、 b 的节点电压分别是 
和 
，列写节点电压方程，
节点 a ： 
节点 b ： 
代入参数并整理，得
则
， 
所以，
因此，
， 
例 7.4-3 电路如图 7.4-3 所示，已知电压源 
，求电流 
。
解：这是一个含有受控源的单回路电路，用相量法分析时，也可将受控源当独立源处理。
由 KVL 得，
代入参数，得
则
