一、 RLC 串联电路的零输入响应
电路如图 6.1-1 所示， 
时，开关 S 处于位置 1 ，且电路已处于稳态，
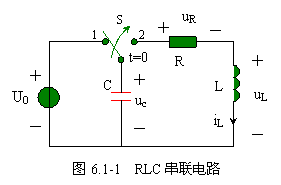
设 
， 
。 t=0 时开关拨到位置 2 ，现讨论 
时响应的变化规律。
时， 
， 
。
电路换路后，由 KVL 得
这是二阶齐次线性微分方程，其特征方程为
特征根为
微分方程的解有如下形式：
其中， A1 、 A2 是待定的常数，可由电路的初始状态确定，
得
， 
所以， RLC 串联电路的零输入响应为
结 论
RLC 串联电路的零输入响应的变化规律取决于两个特征根 
，特征根 
只与电路的结构和参数有关，而与外加激励和电路的初始状态无关，特征根是决定动态电路响应变化规律的重要参数，也称为电路的固有频率（ natural frequency ）。
称为 RLC 串联电路的衰减系数（ attenuation factor ）， 
称为 RLC 串联电路的谐振角频率（ resonant angular frequency ）。
1 、过阻尼情况（ over-damped case ）
 |
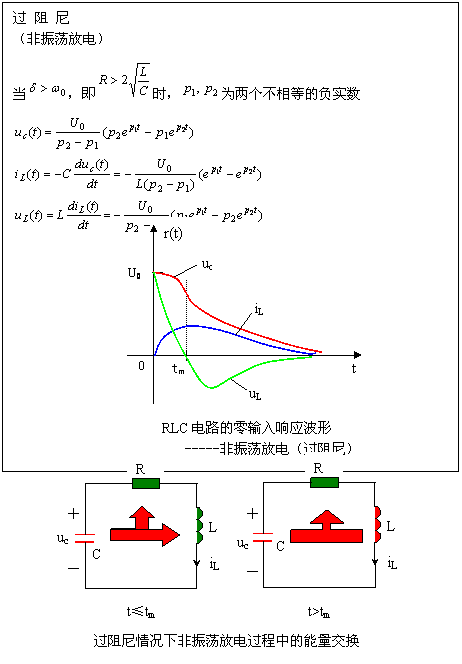2 、欠阻尼情况（ under-damped case ）
 |
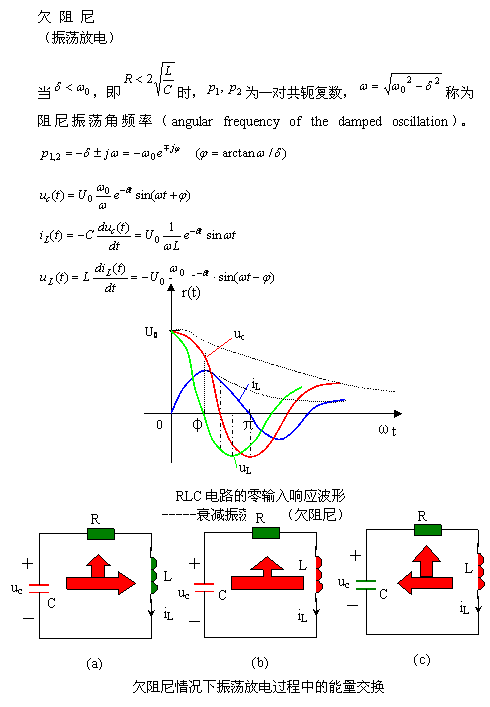3 、无阻尼情况（ undamped case ）
无 阻 尼
（等幅振荡）
当 
，电路中只有电容和电感时，称为无损耗电路。衰减系数 
， 
， 
，特征根 
为一对共轭虚数。
正弦波的振幅不会衰减，作等幅振荡（ unattenuated oscillation ）。
4 、临界阻尼情况（ critically damped case ）
临 界 阻 尼
（非振荡放电）
当 
，即 
时， 
，为两个相等的负实数。
RLC 串联电路的零输入响应
对于 RLC 串联电路，求出衰减系数 
和谐振角频率 
，判断电路零输入响应的性质：
过阻尼、临界阻尼………非振荡放电
欠阻尼………衰减振荡放电
无阻尼………等幅振荡
例 6.1-1 图 6.1-2 所示电路中， 
， 
， 
， 
时开关 S 处于位置 1 ，且电路已处于稳态，电感的储能为 0 。 
时开关拨到位置 2 。（ 1 ）求 
时的 
和 
；（ 2 ）若 
、 
不变，欲使电路在过阻尼情况下放电，问电阻 
应为多少？
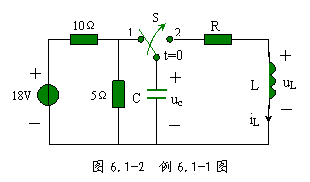
解：（ 1 ）在 
时刻，电路已处于稳态，所以电容相当于开路，则
又电感的储能为 0 ，则
因为
， 
所以 
，欠阻尼，零输入响应为衰减振荡放电。又
， 
因此，零输入响应为
（ 
）
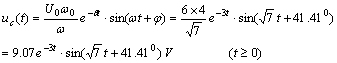
（ 2 ）欲使电路在过阻尼情况下放电，则 
，即
所以，
 |
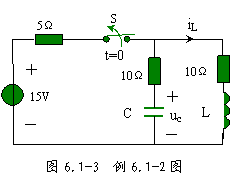例 6.1-2 图 6.1-3 所示电路中， 
， 
， 
时电路已处于稳态， t=0 时开关打开，求 
时的 
。
解： 
时电路已处于稳态，所以把电容当开路处理，把电感当短路处理，并由换路定则得电路的初始状态，
时，开关打开，这时的电路相当于零输入的 RLC 串联电路，其中 
，则
， 
所以 
，过阻尼，零输入响应为非振荡放电，特征根为
故
利用初始状态确定 
和 
，
解得
， 
因此，
（ 
）
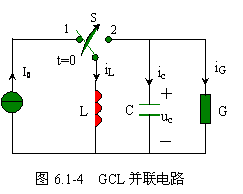
二、 GCL 并联电路的零输入响应
图 6.1-4 所示电路是 GCL 并联电路， 
时开关处于位置 1 ，电路已达到稳态， 
时开关拨到为位置 2 。设 
， 
，现讨论 
时响应的变化规律。
 |
特征根为
令 
，称为 GCL 并联电路的衰减系数， 
，称为 GCL 并联电路的谐振角频率，则
GCL 电路的零输入响应为
GCL 并联电路的零输入响应
对于 GCL 并联电路，求出衰减系数 
和谐振角频率 
，判断电路零输入响应的性质：
当 
，即 
时，过阻尼………非振荡放电
当 
，即 
时，欠阻尼………衰减振荡放电
当 
，即 
时，临界阻尼………非振荡放电
当 
，即 
时，无阻尼………等幅振荡