一、耦合电感元件的相量模型
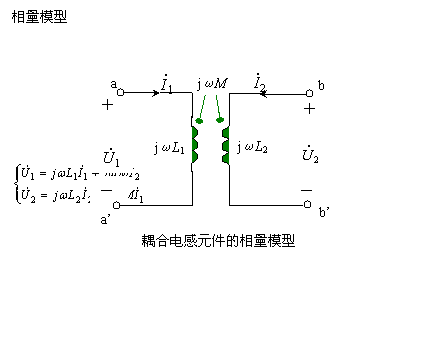
二、耦合电感的去耦等效
出发点
两个线圈之间存在磁耦合，每个线圈的电压不仅与本线圈的电流变化率有关，而且与另一个线圈的电流变化率有关，其伏安关系中的正、负号又取决于同名端的位置及电压、电流的参考方向等。所以，对含有耦合电感的电路的分析就相对比较复杂。
耦合电感在一定的条件下存在去耦等效电路。对某些特定结构的耦合电感作去耦等效，找出其相应的去耦等效电路，使电路的分析得以简化。
1、串联的去耦等效
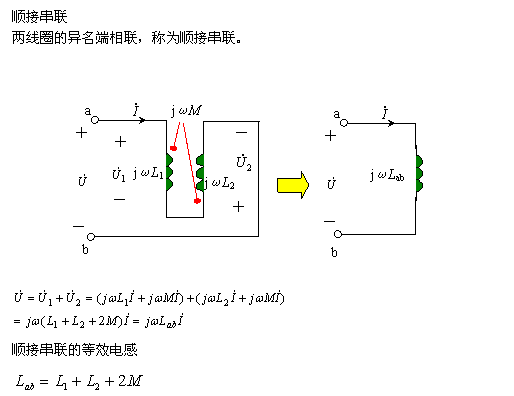
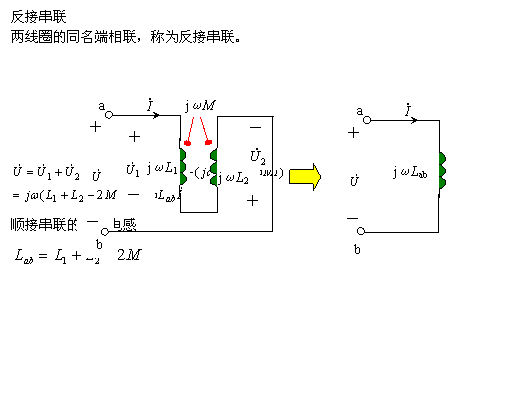
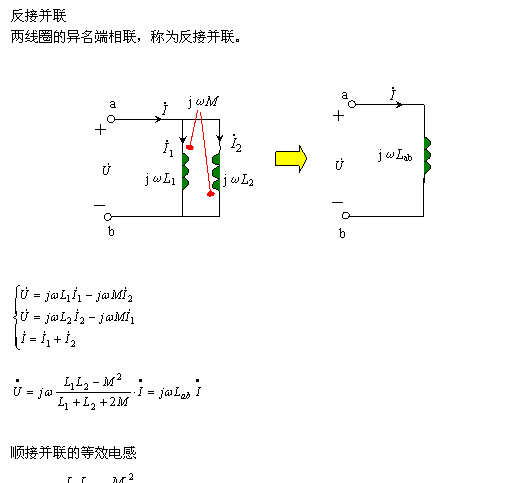
2、并联的去耦等效
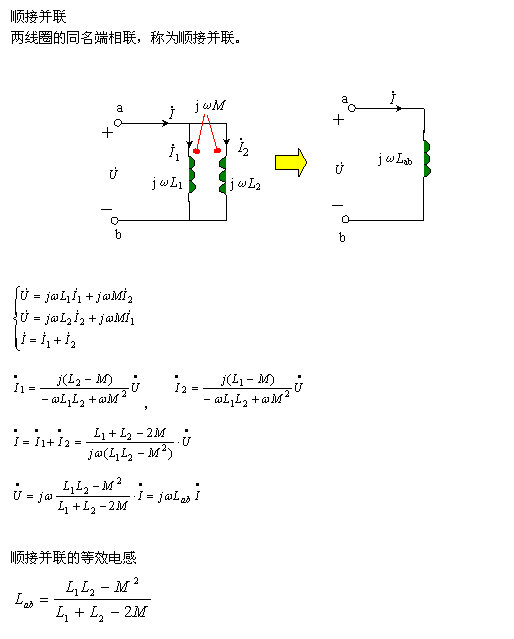
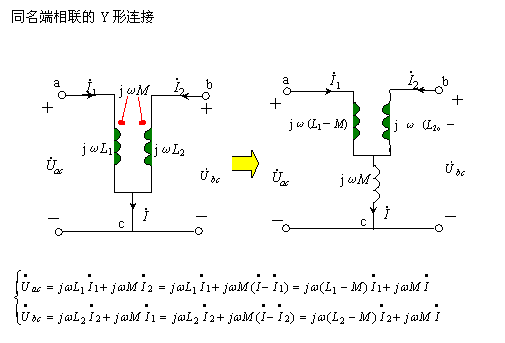
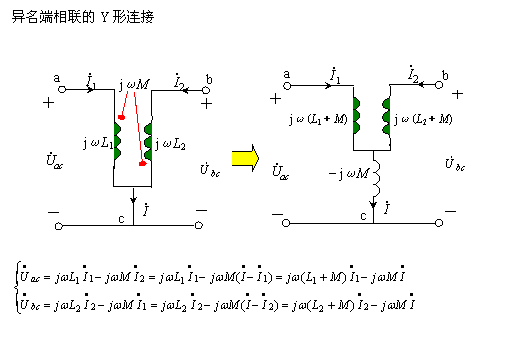
3、Y形连接的去耦等效
三、含有耦合电感的正弦稳态电路分析
思 路
含有耦合电感的正弦稳态电路的分析，依然采用相量法，只是要注意耦合电感的特点。为了使分析和计算简化，如果能去耦等效的，那么先对它去耦等效，得到去耦后等效电路。这样电路中的就不存在耦合电感，只有自感，等效后的电路与第7章的正弦稳态电路并无区别，当然其分析的方法也就一样；如果耦合电感不能去耦等效，那么，就根据耦合电感的基本概念和同名端的位置，列写电路方程，并进行计算。
例8.2-1 图8.2-1（a）所示的正弦稳态电路中，电压源
，
，
，
，
，
，
，
。求电容C上的电压
。
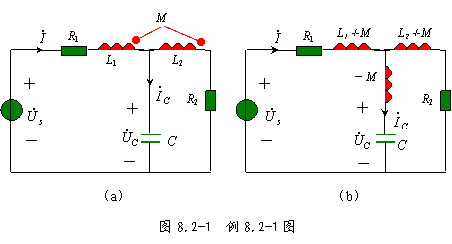
解：图8.2-7（a）电路的耦合电感是异名端相联，作Y形去耦等效，其等效电路如图8.2-7（b）所示。
电阻R2和电感（L2＋M）串联后的等效阻抗为
电感（－M）和电容C串联后的等效阻抗为
则电路的总等效阻抗为
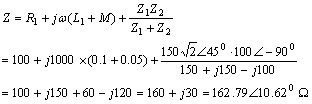
所以，
由分流公式，得电容电流为
则
因此，电容电压为
例8.2-2 电路如图8.2-8（a）所示，已知
，
，
，电感
，
，互感
，负载
可调。问负载为何值时获得最大功率？并求最大功率。
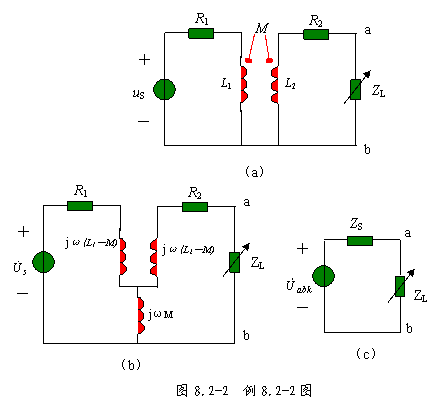
解：对图8.2-8（a）电路作去耦等效，得图8.2-8（b）所示的等效电路。
图8.2-8（b）中，电压源
，用戴维南定理求a、b两端左边电路的等效电路。先求a、b两端的开路电压
，由于a、b两端开路，电阻R2和感抗jω(L2－M)上没有电压，那么，开路电压
就等于感抗jωM上的电压，由分压公式得
再求戴维南等效阻抗
，将电压源短路，则
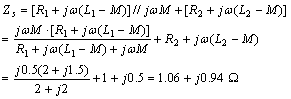
所以，用戴维南定理等效后的等效电路如图8.2-8（c）所示。
由最大功率传输定理，当负载阻抗与等效内阻抗共轭匹配时，负载获得最大功率，则负载阻抗为
最大功率为
四、空心变压器
空心变压器是绕在非铁磁芯上的两个耦合线圈。其中，一个线圈作为输入，接入电源或信号源，称为原边电路或初级电路（primary circuit），另一个线圈作为输出，接入负载，称为副边电路或次级电路（secondary circuit）。
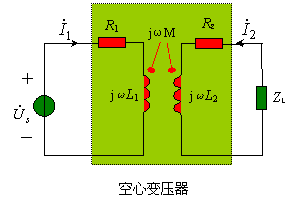
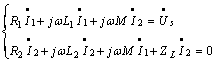
令
，是原边电路阻抗，
，是副边电路阻抗，其中是负载阻抗，
是互感阻抗。则
解得：
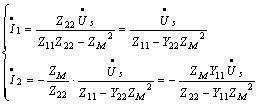
式中，
，是原边电路导纳，
，是副边电路导纳。
原边电路的输入阻抗为
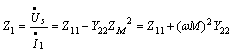
结 论
空心变压器的原边输入阻抗中，除了原边本身的阻抗
外，还包含了由互感和副边电路导纳决定的阻抗，即
，它是反映副边电路通过互感对原边电路产生影响的一个阻抗，称为反射阻抗。
由于，则
，这就说明，如果副边电路阻抗
是感性的，则反映到原边输入阻抗中的反射阻抗是容性的；反之，如果副边电路阻抗是容性的，则反射阻抗是感性的。