同步发电机负载运行和电枢反应

一、负载后磁势分析

• 空载时，I_f→F_f(机械旋转磁势)→F_f→E₀

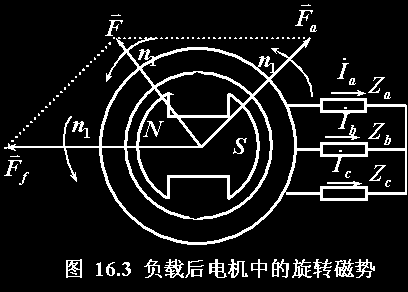
• 负载后，I_a→F_a(电气旋转磁势)。

• F_f/F_a转速均为n₁,转向一致，F_f+F_a=F(合成磁势)。

• 气隙磁场B_d可以看成是由F所建立。B_d也是转速为n₁的旋转磁场。

• 负载后，磁势和磁场将发生显著变化，这一变化主要由电枢磁势的出现所致。

二、电枢反应的概念与内功率因数角

• F_a的存在，将使气隙磁场的大小和位置发生变化，这一现象称为电枢反应。电枢反应会对电机性能产生重大影响。

• 简单地说，电枢反应就是F_a对F_f的影响，这种影响分为增磁、去磁或交磁。

• F_a和F_f之相角差决定了电枢反应的性质。

• F_f为励磁绕组产生的/与A相绕组匝链的磁通，F_f在A相绕组中产生的感应电势E₀滞后于F_f90度。在图示的瞬间，F_f过零点而E₀达到最大值。

• 当F_f与A相轴线重合时，F_f产生的磁通全部与A相绕组匝链，所以F_f也达到其最大值。在图示的瞬间,F_f与A相轴线正交，所以F_f达到零点。可见F_f和A相轴线的夹角与F_f同时变化。

• 若以直轴d同时作为时间相位和空间相位的0点，在图示瞬间，F_f和F_f相位角均为0，E₀的相位角永远滞后F_f 90度。

• 如果I_a与E₀的相位差(由负载性质决定)为0，则I_a的相位角也是滞后90度，达到其最大值。

• 当I_a达到最大值时，F_a将处于A相绕组的轴线(交轴)上，F_a的相位角也是滞后90度。

• 如果I_a与E₀的相位差不为0，而是滞后于E₀一个y角，则F_a也将滞后于A相轴线一个y角。

• 可见I_a在时间相位上滞后于E₀的角度y就等于F_a在空间相位上滞后于A相轴线的角度。在图示的瞬间F_a滞后于F_f（ 90+y）度。

• 由于F_a和F_f在空间相对静止，所以在任意瞬间，F_a均滞后于F_f（ 90+y）度。

• 可见y角决定了F_a与F_f之间的相位差。y角称为内功率因数角。

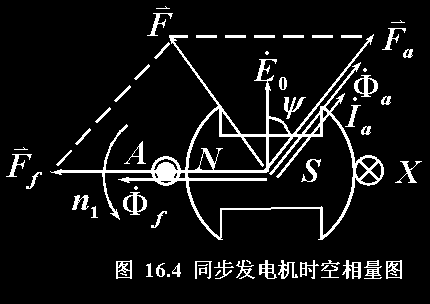
三、不同负载时电枢反应分析

(1)y = 0或者180°

• 此时F_a和F_f之夹角为90/270° ，F_a作用在q轴上，使合成磁势F的轴线位置产生一定的偏移，幅值发生一定的变化。这种作用在交轴上的电枢反应称为交轴电枢反应，简称交磁作用。

(2)y = 90°

• 此时F_a和F_f之夹角为180°，电枢反应为直轴去磁电枢反应。

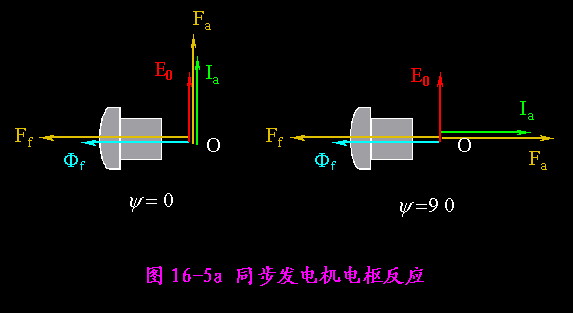
(3)y = -90°

• 此时F_a和F_f之夹角为0° ，电枢反应为直轴增磁电枢反应。

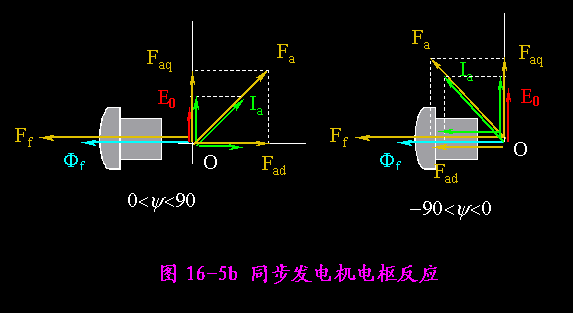
(4)一般情况下的电枢反应

• 将I_a分解为I_d/I_q, 分别产生F_ad/F_aq。

I_a=I_d+I_q

I_d=I_asiny

I_q=I_acosy

F_a=F_ad+F_aq

F_ad=F_asiny

F_aq=F_acosy

• F_ad/F_aq分别产生d轴和q轴电枢反应。　

• 说明：（1）绕组的感应电势 永远落后于它所匝链的磁通90° ；

  （2）时-空统一相量图：因为空间向量（主要指F_f、F_a、F_R 、F）与时间相量（主要指F、U、E、I_a）均以同步速旋转，电机运行过程中此关系不变；因为I_A达最大值时，电枢合成磁势幅值位置也恰在A相绕组的轴线上，故I_a与F_a规定重合在一起； 只要是随正弦规律变化的基波量均可统一为相量图来表示。　

• 在时空相量图中F_f和F_f 处于d轴，E₀滞后于d轴90°,处于q轴，I_a和E₀之间的相位差y由负载性质决定，F_a和F_f重合。

• 利用时空相量图分析不同负载情况时同步发电机电枢反应的情况甚为方便。　

四、电枢反应电抗和同步电抗（Synchronous Reactance）

• 负载后,F_a将在电机内部产生跨过气隙的电枢反应磁通F_a和不通过气隙的漏磁通F_s,分别在电枢各相绕组中感应出电枢反应电势E_a 和漏磁电势E_s。

• 不计饱和时,E_a与电枢电流I_a成正比,比例常数称X_a为电枢反应电抗。考虑到相位关系后，每相电枢反应电势为：
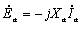  　　　　　　　　　　　E_a=-jX_aI_a

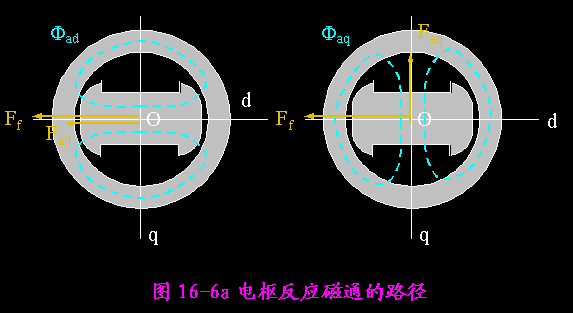
• X_a和F_a所经过磁路的磁阻成反比。对于凸极电机而言,当F_a和F_f重合时,F_a经过直轴气隙和铁心而闭合(直轴磁路);该路径磁阻较小,对应的X_a就较大。

• 当F_a和F_f正交时,F_a经过交轴磁路而闭合。磁阻较大,所以X_a较小。

• 一般情况下,F_a和F_f之间的夹角由负载的性质决定,为90+y,F_a的流通路径介于直轴磁路和交轴磁路之间，X_a的大小也就介于最大和最小之间。

• 不同负载对应的X_a也不同,这给分析问题带来了诸多不便。为了解决这一问题,人们采用了正交分解法和叠加原理,将F_a看成是其直轴分量F_ad和交轴分量F_aq的叠加,并认为单独激励直轴电枢反应磁通F_ad,对应有一个固定的直轴电枢反应电抗X_ad,并在定子每相绕组中产生直轴电枢反应电势E_ad;F_aq单独激励交轴电枢反应磁通F_aq,对应交轴电枢反应电抗X_aq,产生交轴电枢反应电势E_aq。

E_a=E_ad+E_aq=-jX_adI_d-jX_aqI_q　 (16-4)

• 考虑到F_s引起的漏抗电势E_s=-jX_sI_a后,电枢绕组中由I_a引起的总的感应电势为
  　　　　E_a+E_s=-jX_adI_d-jX_aqI_q-jX_sI_a
  　 =-jX_adI_d-jX_aqI_q-jX_s(I_d+I_q)
  =-j(X_ad+X_s)I_d-j(X_aq+X_s)
  =-jX_dI_d-jX_qI_q　　　

• 其中X_d=X_ad+X_s定义为直轴同步电抗，X_q=X_aq+X_s定义为交轴同步电抗。

• 对于隐极电机来说，由于电枢为圆柱体，可以认为直轴磁路和交轴磁路的磁阻相等，则X_ad=X_aq=X_a ：
  　　　　E_a+E_s=-jX_aI_d-jX_aI_q-jX_sI_a
  　 =-jX_aI_a-jX_sI_a
  =-j(X_a+X_s)I_a
  =-jX_sI_a　　　　　　　(16-6)

• 式中X_s=X_a+X_s定义为隐极电机的同步电抗。

• 由定义可知，同步电抗包括两部分：电枢绕组的漏电抗和电枢反应电抗，又称为主电抗和漏电抗。 X_s、X_a随着饱和程度的增加而减小；X_s不随饱和程度的变化而改变，X_s比X_a小得多。