一、短路特性
- n=n1/电枢绕组三相持续短路/然后加励磁电流，称为稳态短路运行。
- 这时U=0，如果改变If，则短路电枢电流Ik也改变。Ik=f(If)就是短路特性。
- 短路运行时，Ik和E0之间的相位差y仅由Xs和绕组电阻决定，忽略电阻时，Ik将滞后于E090电角度，其电枢反应表现为直轴纯去磁作用。
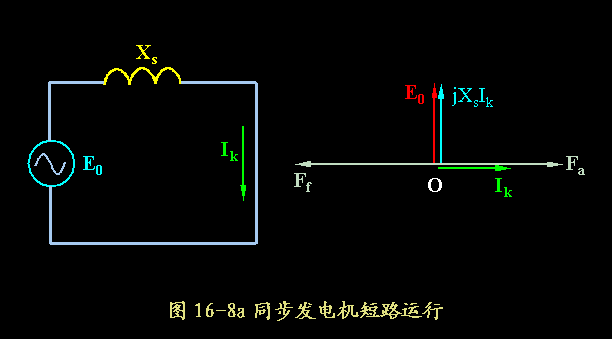
- 去磁作用减少了电机中的磁通，磁路不饱和E0=f(If)呈线性。由于短路电流Ik=-jE0/Xs 所以Ik=f(If)也呈线性，是一条通过原点的直线。
- 稳态短路时，电机中的电枢反应为直轴纯去磁作用，电机的磁通和感应电势较小，短路电流也不会过大，所以三相稳态短路运行没有危险。
- 对凸极电机来说，短路时交轴电枢磁势Fq=0 分析时只需将Xs用Xd、将Ia用Id代替即可。
二、利用Ik=f(If)和E0=f(If)求Xs/Xd
- 短路且略去电阻压降时，
E0=-jXsIk
Xs=E0(If)/Ik(If) - 测定同步电抗的简单方法：
① 用原动机带动同步发电机在同步转速下运转，测取E0=f(If)和Ik=f(If)特性。
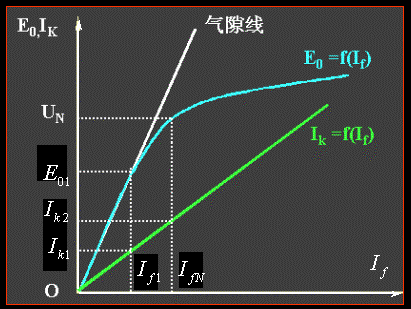
② E0=f(If)和Ik=f(If)绘成曲线，并在E0=f(If)上作出气隙线。
③选取某一If，求得对应的短路电流Ik1和对应于气隙线上的电势E01，则
不饱和Xs()=E01/Ik1 - 在E0=f(If)求得对应于额定电压UN的励磁电流IfN，再从Ik=f(If)上求得对应于IfN的短路电流Ik2，则
饱和Xs(Xd)=UN/Ik2 - 凸极电机的Xq可以利用经验公式求得
Xq≈0.65Xd
三、零功率因数负载特性
- 负载特性是指当负载电流Ia=常数，功率因数cosj =常数的条件下，端电压U与励磁电流If的关系。
- 对应于cosj=0 & Ia=IN时一条负载特性称为零功率因数特性。
- cosj=0的负载为纯电感负载，即y=90度，Id=Ia，Iq=0,且
U=E0-XdId=E0(If)-XdId=E0(If)-XdIN - 已知空载特性E0(If)和同步电抗Xd(或Xs)的情况下，就可以作出同步电机的零功率因数特性曲线。反过来通过测取空载特性和零功率因数特性就可以求得同步电抗，经过进一步的处理，还可以求得定子漏抗。
四、同步电抗和定子漏抗
- 同步电抗
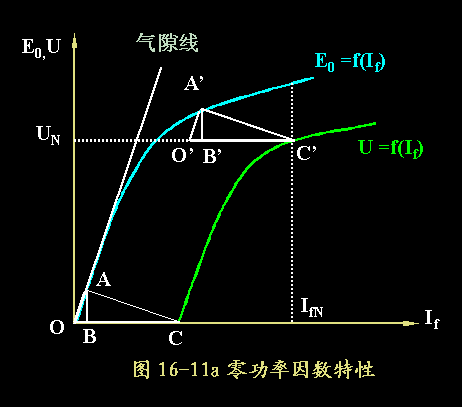
在零功率因数特性曲线上取出对应于U=UN的IfN，再在空载特性曲线上取出对应于IfN的空载电势E0N，则 Xd=(E0N-UN)IN - 定子漏抗
U=0时，对应于零功率因数特性上的励磁电流If=OC=OB+BC，OB段用来产生漏抗电势Es=AB=XsId。BC段用来产生电枢电势Ead=XadId，可见△ABC的BC边代表纯去磁的电枢反应磁势，AB边代表定子漏抗。由于BC和AB的长度均和电枢电流Id成正比。所以当Id一定时，△ABC是固定的，此三角形称为同步电机的特性三角形。
只要求得特性三角形，我们就可以很方便地求得定子漏抗，即
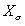Xs=AB/Id
- 特性三角形的作法:(动画)
Id一定时，△ABC是固定的，在空载特性曲线上移动△ABC的顶点A时，C的轨迹即为零功率因数特性。如果我们在零功率因数特性曲线上向上平移△ABC的顶点C到额定电压UN时，将得到△A'B'C' ，并且O'C'=OC,O'A'//OA，由此可得到特性三角形的作法：
①在额定电压UN处作一水平线交零功率因数曲线于C'，截取O'C'=OC ；
②过O'作OA的平行线交空载特性曲线于A'；
③过A'作A'B'⊥O'C'于B'，则△A'B'C'即为特性三角形
五、外特性和电压调整率
- 外特性是指：n=n1,If=常数,cosj=常数的条件下，同步发电机作单机运行时,端电压U随负载电流Ia而变化的关系,即U=f(Ia)曲线
-
外特性曲线的走向和负载的性质有关。对于感性负载(j>0)，在励磁电流不变的情况下，随着Ia增大，有两个因素导致U下降，其一是电枢反应的去磁作用的增强，其二是漏抗压降的增大，所以感性负载时，同步电机的外特性是下降的曲线。
-
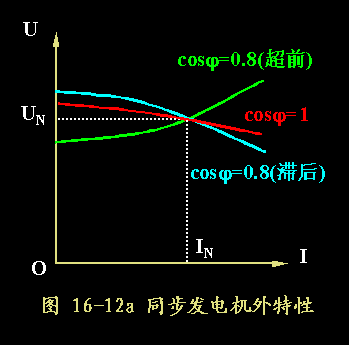
- 对于j<0,的容性负载，电枢反应可能表现为增磁作用，随着Ia增大，U可能会上升
- 保持额定励磁电流IfN和转速n1不变,将发电机的完全卸载,发电机的端电压将由UN变化为空载电势E0，电压变化的幅度可以用电压调整率来表示
DU=(E0-UN)/UN - DU是发电机的性能指标之一，按国家标准规定不能大于40% 。