一、概述
gps相对定位，就是在不同观测点（站）上安置GPS接收机，同步观测相同的GPS星座，用以测定各观测站在WGS－84坐标系中的相对位置（即三维坐标增量或称为基线向量）的方法。
根据相对定位时GPS接收机所处的状态不同，相对定位可划分为静态相对定位和动态相对定位两类。
二、GPS静态相对定位
（一）GPS静态相对定位的原理方法及其应用
GPS静态相对定位的一般方法，就是将一台GPS接收机安置在已知坐标的地面点（已知点）上，另一台或多台GPS接收机安置在未知坐标的地面点（待定点）上，并保持各接收机固定不动，同步连续观测相同的GPS卫星星座，用以求得未知点相对于已知点的坐标增量（基线矢量），从而由已知点坐标，推求各未知点坐标的方法。
（二）静态相对定位观测方程
1、基本观测量及其差分形式
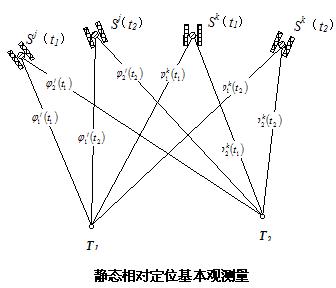
设安置于某一GPS基线两端点上的接收机Ti (i=1,2)，在观测历元T1和T2对卫星Sj和Sk进行了同步观测，则可得到独立的载波相位观测量（基本观测量）：
、
、
、
、
、
；
、
、
、
。
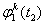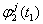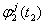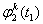设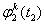
、
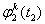和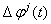
分别代表不同接收机之间，不同卫星之间和不同观测历元之
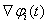
间的观测量之差，即
由公式（5－23）知，观测方程的一般形式为
在GPS相对定位中，常用的三种差分（线性组合）是单差（分）、双差（分）和三差（分），它们定义如下：
（1）单差（SD―Single Difference）：
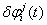
它是在同一观测历元下，不同测站、同步观测相同卫星的观测量之差。
（2）双差（DD―Dual Difference）：
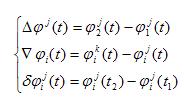
它是在一观测历元下，不同测站、同步观测一组卫星的单差之差。
（3）三差（TD―Triple Difference）：
它是不同历元、不同测站、同步观测一组卫星，求得的双差之差。
2.单差观测方程
3.
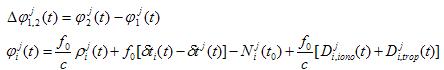
式中，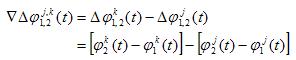
，
，
，
。
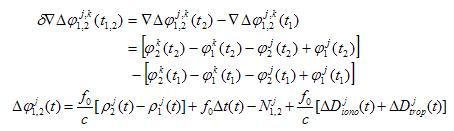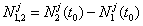从上式可见，单差观测方程中，卫星钟差的影响被消除了，而两测站接收机的相对钟差（钟差之差）Δt(t)，对于同一观测历元来说，与其它被测卫星组成的单差观测方程，都是相同的。又由于卫星轨道误差和大气折射误差，对同步观测的两测站具有一定的相关性，因此，在测站间求单差后，它们的影响将明显减弱，特别是对于短基线（S＜20km），效果更显著。
由以上讨论可知，单差观测模型的优点是：消除了卫星钟差的影响，并明显削弱了卫星轨道误差和大气折射误差的影响，但单差观测方程个数比独立观测量方程减少一半。
3、双差观测方程
若在求单差分的基础上，再对不同卫星Sj、S k求差，便可得到双差观测方程。可得：
式中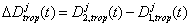
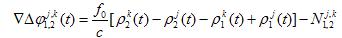
由双差观测方程可见，接收机相对钟差Δt(t)被消除了，这是双差观测模型的重要优点。因为GPS接收机使用稳定性较差的石英钟，它难以用模型表示。如果将每个观测历元的接收机钟差都作为未知数求解，则将使解算基线向量的法方程中的未知数个数大大增加。使用双差模型后，接收机钟差的影响被消除了，它既不涉及钟差模型，又使法方程中未知数个数大大减少，很方便地解决了GPS数据处理中一个棘手的问题。所以，几乎所有的GPS基线解算软件，都使用双差观测模型。但双差观测模型的方程个数比单差模型减少，对解算精度可能造成不利影响。
4、三差观测方程
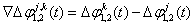
所谓“三差”，就是在“双差”的基础上，再对两个不同观测历元t1和t2求差：
由三差观测方程可知，求三差后，观测方程中不再包含整周未知数Ni(t0)和Nk(t0)，这是三差模型的优点，但三差观测方程的个数比双差模型又进一步减少；且求三差后，相位观测值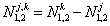
的有效数字位大为减少，增大了计算过程的凑整误差，这些将对未知参数的解算产生不良影响。所以，三差模型求得的基线结果精度不够高，在数据处理中，只作为初解，用于协助求解整周未知数N（t0）和周跳等问题。