一、高程系统
大地高系统
大地高系统是以参考椭球面为基准面的高程系统。某点的大地高是该点到通过该点的参考椭
球的法线与参考椭球面的交点间的距离。大地高也称为椭球高，大地高一般用符号H表示。大地高是一个纯几何量，不具有物理意义，同一个点，在不同的基准下，具有不同的大地高。
正高系统
正高系统是以大地水准面为基准面的高程系统。某点的正高是该点到通过该点的铅垂线与大地水准面的交点之间的距离。
正常高系统
正常高系统是以似大地水准面为基准的高程系统。某点的正常高是该点到通过该点的铅垂线与似大地水准面的交点之间的距离。
二、gps大地高的应用问题
（一）大地高与正常高（正高）的关系：
若定义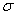
、
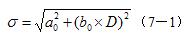和
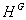分别代表大地高、正常高和正高；
、
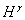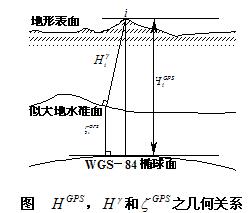
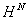分别代表高程异常和大地水准面差距，则它们的几何关系如图所示。
由图可知
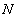
上式是个近似关系式，严格讲应顾及地球椭球面法线与铅重线方向之差异，但该差异一般不大于1′[17]，因此，由它所引入的误差不大于0．1mm，完全可忽略不计。如此，正常高和正高可表示为：
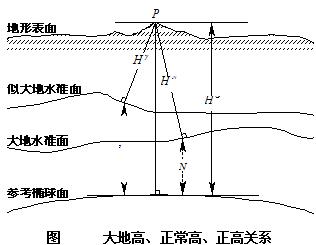
因为大地水准面差距N，在陆地上只能近似求得，而高程异常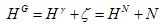
可以通过天文重力水准方法较精确求得，所以，高程通常采用正常高
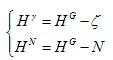来度量。在下面我们只研究GPS水准测定正常高的问题。
可通过GPS三维定位方法测定。但由于GPS单站定位误差较大，因而必须采用差分GPS
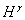
定位方法。另外，GPS测量所使用的WGS－84坐标系与我们所使用的局部地方坐标系的椭球大小、形状和定位不一致，故不能直接由GPS大地高来计算正常高。解决的办法通常是在所施测的GPS网中联测若干已知正常高的GPS点（该点称为GPS水准控制点），并由它们求得相对于WGS－84椭球的高程异常值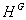，然后再推求那些未知正常高的GPS点的正常高。
由图可得
（二）求解GPS测站正常高的方法
设GPS基线向量网经三维无约束平差后求得各GPS点的大地高平差值为
,又已知网中
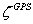
有m个点已知其正常高为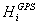
,则得网中m个点的高程异常值
下面，我们讨论如何由求得的m个GPS水准控制点的高程异常值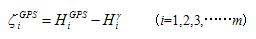
,来推求网中其它没
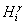
有水准资料的j个GPS点的正常高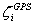
的问题，也即推求局部似大地水准
面形状的问题。
目前，求解的方法有：等值线图内插法、局部系统转换法，平面拟合法、曲面拟合法、离散点加权平均法、多面函数法、样条函数法等等。在这些方法中，应用得较广泛的是加权二次曲面拟合法。下面就此法加以讨论。
对于不太大的区域，似大地水准面的形状可表示为平面坐标x、y的函数
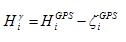
而模型参数矩阵X可写成
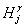
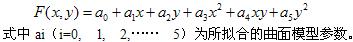
可见，解算方程至少需要6个GPS水准控制点，如果多于6个点，可按最小二乘原理求解模型参数ai；如果只有三个点，则是平面拟合法；当取P1＝P2＝……＝Pm＝1时，则是等权二次曲面拟合法。
求得模型参数ai后，便可将待定正常高的GPS点j的平面坐标xj、yj代入上式，求得其正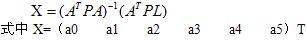
三、用曲面拟合法求正常高的几点说明与建议
（一）GPS水准控制点的分布与密度问题
GPS水准控制点的分布与密度是否合理，将直接影响正常高的拟合精度。应根据实际情况加以确定。
（1）平坦地区，高程异常值变化平缓，只需测定少量（不少于3个）较均匀分布于测区的GPS水准控制点，采用平面拟合法。拟合精度一般优于10cm。
（2）丘陵地或小山区，高程异常变化较大，在这种条件下，GPS水准控制点均匀分布是不可取的，高程异常值变化大的地方，要适当增大GPS水准控制点的密度，并采用曲面拟合方法。
（3）GPS水准控制点不应在某一区域分布过密，否则，在加权拟合正常高时，将会扭曲所拟合的似大地水准面形状。
（二）拟合区域外的GPS点的正常高，其精度将会下降，应尽量避免出现这种情况。为此，对于较大面积（＞300km2）的GPS网，其四周和中部都应有GPS水准控制点；而面积较小的GPS网，则在其周边布测若干个GPS水准控制点即可。
（三）为获得好的拟合结果，应避免采用三角高程点作为GPS水准控制点，因为它的高程误差可大至分米量级。在水准联测困难的山区，建议采用：“同步对向精密垂直角观测”方法[18]，测定GPS水准控制点的高程，使其精度优于0．1米。
（四）对于地形复杂（例如部分为平地、部分为山区）的测区，拟合时可分区拟合，分别求解平地与山区的模型参数ai,即用不同形状的数学面来拟合不同地区的似大地水准面。
（五）对于地形起伏较大的山区，如果附加由重力资料建立起来的地球模型，并进行地形改正，则曲面拟合法也可获得厘米级精度的正常高。
（六）在地势较平坦的小区域内，用GPS水准拟合法，拟合似大地水准面的精度，可代替三、四等水准测量。