1、逐点比较法圆弧插补
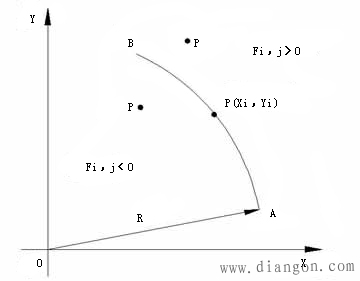
圆弧AB的圆心O(0,0),半径R,加工点坐标为P(xi,yj),则圆弧插补偏差判别函数为
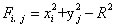
当Fi,j=0时,点在圆弧上;当Fi,j>0时,点在圆弧外;当Fi,j<0时,点在圆弧内。将Fi,j=0归于Fi,j>0
1、插补第一象限逆圆弧
(1)Fi,j≥0时
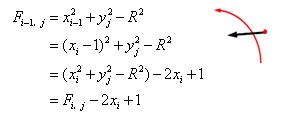
(2)Fi,j<0时
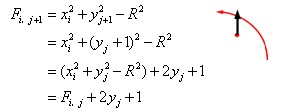
2、插补第一象限顺圆弧
(1)Fi,j≥0时
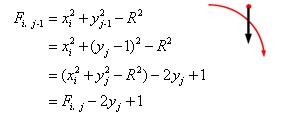
(2)Fi,j<0时
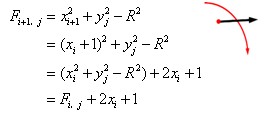
注意:xi、yj的值在插补过程中是变化的,这一点与直线插补不同。
终点判别方法:
1、判别插补或进给的总步数
2、分别判别各坐标轴的进给步数
第I象限逆圆插补流程:
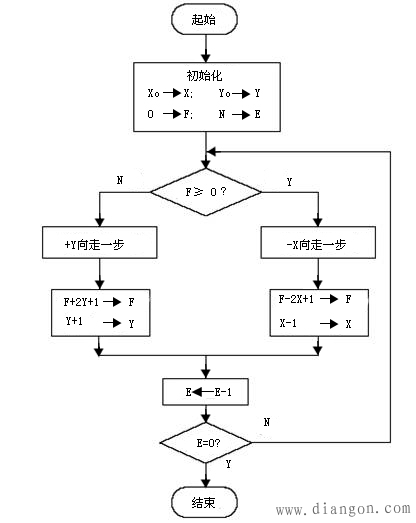
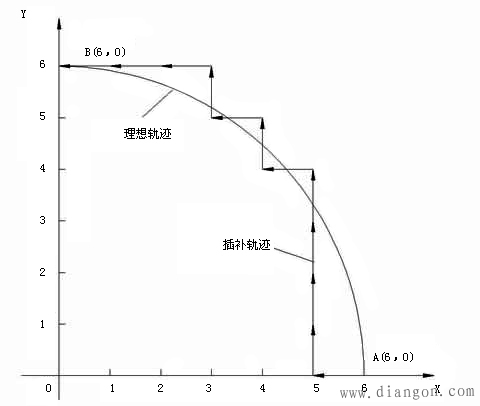
例5-2 设加工第一象限逆圆弧AB,起点A(6,0),终点B(0,6)。试用逐点比较法对其进行插补并画出插补轨迹图。
终点判别寄存器E=6+6=12,每进给一步减1,E=0时停止插补。
|
步数 |
偏差判别 |
坐标进给 |
偏差计算 |
坐标计算 |
终点判断 |
|
起点 |
F0,0=0 |
x0=6y0=0 |
E=12 | ||
|
1 |
F0,0=0 |
-X |
F1,0= F0,0-2x0+1=0-12+1=-11 |
x1=6-1=5y1=0 |
E=11 |
|
2 |
F1,0<0 |
+Y |
F1,1= F1,0+2y1+1=-11+0+1=-10 |
x2=5y2=0+1=1 |
E=10 |
|
3 |
F1,1<0 |
+Y |
F1,2= F1,1+2y2+1=-10+2+1=-7 |
x3=5y3=1+1=2 |
E=9 |
|
4 |
F1,2<0 |
+Y |
F1,3= F1,2+2y3+1=-7+4+1=-2 |
x4=5y4=2+1=3 |
E=8 |
|
5 |
F1,3<0 |
+Y |
F1,4= F1,3+2y4+1=-2+6+1=5 |
x5=5y5=3+1=4 |
E=7 |
|
6 |
F1,4>0 |
-X |
F2,4=F1,4-2x5+1=5-10+1=-4 |
x6=5-1=4y6=4 |
E=6 |
|
7 |
F2,4<0 |
+Y |
F2,5= F2,4+2y6+1=-4+8+1=5 |
x7=4y7=4+1=5 |
E=5 |
|
8 |
F2,5>0 |
-X |
F3,5= F2,5-2x7+1=5-8+1=-2 |
x8=4-1=3y8=5 |
E=4 |
|
9 |
F3,5<0 |
+Y |
F3,6= F3,5+2y8+1=-2+10+1=9 |
x9=3y9=5+1=6 |
E=3 |
|
10 |
F3,6>0 |
-X |
F4,6= F3,6-2x9+1=9-6+1=4 |
x10=3-1=2y10=6 |
E=2 |
|
11 |
F4,6>0 |
-X |
F5,6= F4,6-2x10+1=4-4+1=1 |
x11=2-1=1y11=6 |
E=1 |
|
12 |
F5,6>0 |
-X |
F6,6= F5,6-2x11+1=1-2+1=0 |
x12=1-1=0y12=6 |
E=0 |