电阻的Ｙ形与△形联接及等效变换

电路中电阻用串、并联方法化简为一个等效电阻。这种电路不论有多少电阻，结构有多复杂，都能用串、并联方法化简为一个等效电阻的电路，称为简单电阻电路；但有些电路电阻与电阻的关系，既不串、也不并这种类型的电路称为复杂电阻电路。对于这类电阻可用三角形网络等效变换为星形网络或星形网络等效变换为三角形网络的方法来分析。

一、电阻的Ｙ形与△形联接的概念<?XML:NAMESPACE PREFIX = O />

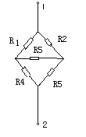
在电路中，有时电阻的联结即非串联又非并联，如图所示中，电阻<?XML:NAMESPACE PREFIX = V /> 的一端都接在一个公共结点上，各自的另一端则分别接到三个端子上，我们称此联结方式为Y形联结；电阻 则分别接在三个端子的每两个之间，我们称之为三角形联结。

二、Y形和△形之间的等效变换

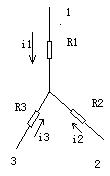
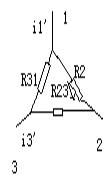
如图所示，设它们对应端之间有相同电压 如果它们彼此等效，则

对于图中 联结的电路，各电阻中的电流分别为

对结点1、2、3分别列KCL方程，有

（1）

而对图 联结的电路，根据广义回路分别列KVL方程，有

又因

求解上述三个方程，可得出

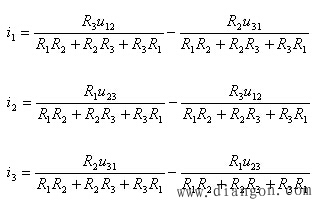
根据等效变换的原则，式（1）和式（2）中电压 、 和 前面的系数应该相应地相等，故经整理后可得

（3）

上式就是从已知的 联结电路的电阻来确定等效 电路的各对应电阻的关系式。

也可整理成

（4）

可见，上式就是从已知的 联结电路的电阻来确定等效 联结电路的各对应电阻的关系式。

如果电路对称，即当　　

　

　 　　

　 则它们之间的变换关系为

关于电阻的 和 之间的等效变换，我们要认真理会其含义并加以记忆，在具体变换过程中，对各等效电阻应出现的位置不能搞错。另外，由于电路图的画法可能不同， 和 可画成不同的形式，我们在使用时一定要仔细加以辨别。

例题：求如图所示中电路的等效电阻 ，其中R为3Ω。

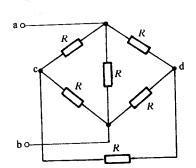
解：将联结于结点C的三个电阻R作 变换，各等效电阻 为

变换后的电路如图（b）所示。在图（b）中

R与 并联等效电阻为

所以