支路电流法就是以支路电流为未知量来列出电路方程，对于任何一个线形或非线形电路，如果我们首先能求出各支路中电流。再求各支路电压或元件两端的电压。其元件产生或消耗的功率都可以迎刃而解。下面以图中电路为例具体说明支路电流法的解题步骤。
一、解题步骤<?XML:NAMESPACE PREFIX = O />
1． 标出各未知支路电流的参考方向
<?XML:NAMESPACE PREFIX = V />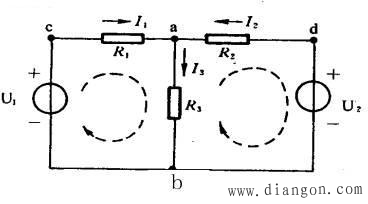
此图中设三条支路的电流为未知量，其参考方向如图所示。
2．根据KCL列出结点电流方程
图中(链接1)有a，b两个结点，分别应用KCL可得到：
节点a： 
节点b：
显然，其中一个方程可由另一个变换而成，即节点电流方程有一个是无效的。
一般来说，一个电路如果有n个节点，则可以列出（n-1）个有效的电流方程式，称为独立电流方程式。
本图中，由于n=2，则上述两式中可任取其一作为独立的电流方程式。
3．根据KVL列出回路电压方程
图中共有三个回路。即abca, adba, adbca..由KVL可列出三个回路电压方程式。但通过分析我们同样发现其中仅有两个回路电压方程式是独立有效的。本图已设三个未知量，共需三个独立的方程。前面已由KCL列出了一个独立的方程。这儿再由KVL列出两个独立的电压方程，正好就满足了全部的要求。
一般情况下，对于具有n个节点，b条支路的电路。由KCL可以列出（n-1）个独立的电流方程。而余下的独立方程数l=b-（n-1）个回路电压方程则可相应地由KVL列出。我们在针对回路列写KVL方程时，如果每个回路中至少包含一个新的支路，则方程就是独立的。
一种较为简便的方法就是按照网孔来列KVL方程，网孔是回路的特殊的形式，它的内部没有其他的支路。图中abca和adba就是两个网孔。而adbca则不是。因为其内部有支路ab。根据有关“网络拓扑理论”的描述可知，电路图中所有网孔就是一组独立的回路，网孔数等于b-（n-1）个。
图中网孔内用虚线标出所选定的回路绕行方向。列出KVL方程连同前面已列出的KCL方程。可得到以下方程组：
4．联系求解方程组
用消元法或行列式来计算未知量。
5．结果检验
将计算出的各支路电流值对所设定的非独立节点列写KCL，或者对未列KVL方程的一个回路进行计算，还可以通过功率平衡关系来检验计算结果的正确性。
支路电流法的不足之处是：当支路的数目较多的时候。方程的数目也相应较多，计算起来较为繁琐。
二、例题
例题1： 在图中，用支路电流法求支路电流
，
和
。
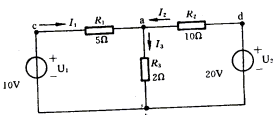
解 选定各支路电流的参考方向如图中所示。
对结点 a，列KCL方程，有
对两个网孔分别列KVL方程，得
将有关数据代如方程组并整理，可得
解得
例题2：在如图所示电路中，已知
。求支路电流
及电流源的端电压 
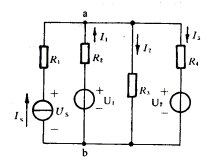
解： 该电路共有四条支路，由于
与
串联，根据电流源的外特性可知， 不会改变此支路中的电流的大小，所以这条支路中电流仍为3A，这时，我们待求的未知变量就变成求解另三个支路电流
。
用支路电流法列出的KCL和KVL方程组为：
联立求解得
另有 
