分析电路时，在支路由于相对于结点数较多的情况下，若用支路法来求解题，由于方程较多，计算工作量较大，此时可以考虑用结点法来求解。
一、结点电压<?XML:NAMESPACE PREFIX = O />
电路中任意选择某一结点为参考结点，即作为零电位点，则其他结点与此参考结点之间的电压称为结点电压。
结点法就是以结点电压为电路的独立变量来建立方程并求解此电路的一种分析方法。结点电压的参考极性均以零参考结点相联结，因此，支路电压就等于相关的两个结点的 电压之差，或者说电路的全部支路电压均可以通过结点电压来表示。
二、结点电压方程
在任意回路中，各结点电压一定会自动满足KVL，故结点电压法中不必再列写KVL方程，只需对除零参考结点外的其他结点（独立结点）应用KCL列出结点电流方程，然后通过支路本身的特性方程把各支路电流用相关的结点电压来表示，这样就可以获取一组与结点数相等的独立结点电压方程，求解这些方程组，即可求得电路的各结点电压，并进一步求出各支路电压和电流。从而达到全面求解电路的目的。
如图所示电路图，结点数n=3,选择点o为零参考点，结点1和2的结点电压分别以<?XML:NAMESPACE PREFIX = V />
和
表示，他们均以O点处为“-”极性，各支路电流的参考方向如图所示。
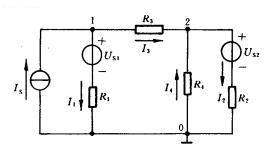
根据KCL有：
结点1： 
结点2： 
考虑各支路方程为：
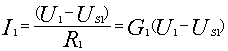
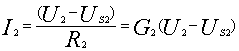
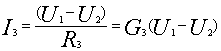
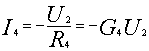
将（2）式代入（1）式整理后得：
即为结点电压方程，联立求解后，即可求解
和
，并代入（2）式后，可求出各支路电流和其他待求量。
三、结点电压方程的一般规律
（3）式写成普遍形式为：
结点1：
结点2；
其中，
称为结点1的自导，是所有联结到结点1上的各支路的电导之和。同样，
称为结点2的自导，是联结到结点2上的各支路的电导之和
，是指结点1和结点2之间所有公共支路中的电导之和的负值，称为结点1和结点2之间的互导。在列结点电压方程时，自导总是正值，互导总是负值，这是由于结点电压正方向一律假定为从该结点指向参考结点的缘故。等式左边也各项就相当于流出该结点的电流之和。
等式右边，
和
是联结到结点1和结点2上的各支路中的电流和电压源分别流入结点1和结点2的电流之和。把正方向流入结点的电流取正号，否则就取负号。等式右边各项相当于流入该结点的电流之和。
对于具有（N-1）个独立的结点的电路，起结点电压方程可按式（4）推广而得。