同步时序逻辑电路的设计

1、设计电路最简的标准是：

1．选用小规模集成电路时，所用的触发器和门电路的数目最少，而且触发器和门电路的输入端数目也最少。

3． 使用中、大规模集成电路时，所用的集成电路数目最少，种类最少，而且互相间的连线也最少。

2、同步时序逻辑电路的设计步骤

一、逻辑抽象，得出电路的状态转换图或状态转换表

1．分析给定的逻辑问题，确定输入变量、输出变量以及电路的状态数。

2．定义输入、输出逻辑状态和每个电路状态的含意，并将电路状态顺序编号。

3．按照题意列出电路的状态转换表或画出电路的状态转换图。

二．状态化简

等价状态：若两个电路状态在相同的输入下有相同的输出，并且转换到同一个次态去。

状态化简目的：合并等价状态，求得最简的状态转换图。

三．状态分配（状态编码）

确定触发器的数目n。为获得时序电路所需的M个状态，必须满足2^n-1 <M<2ⁿ

给每个电路状态规定对应的触发器状态组合，即从2ⁿ个状态中取M个状态。方案可能有多种。

四．选定触发器的类型，求出电路的状态方程、驱动方程和输出方程

选定触发器的类型后，根据状态转换图（或状态转换表）和选定的状态编码，触发器的类型，写出电路的状态方程、驱动方程和输出方程。

五．根据得到的方程式画出逻辑图

六．检查设计的电路能否自启动

如不能自启动，则需采取措施,解决办法为:

1.在电路开始工作时通过预置数将电路的状态置成有效状态循环中的某一种。

2. 修改逻辑程序

下图是设计工作的方框图:

例5.3 试设计一个带有进位输出端的十三进制计数器

解：首先进行逻辑抽象，计数器是属于摩尔型的一种简单时序电路。设有进位输出时C=1，无进位输出时C=0。

设十三个有效状态为S₀S₁S₂……S₁₂电路状态转换图如图5.6所示。

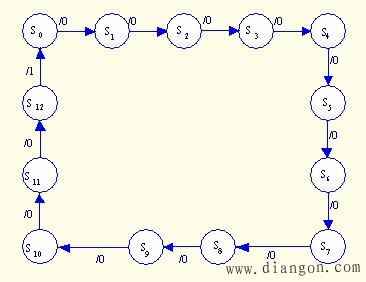
图5.6 例5.3的状态转换图

状态转换图不能再简化。

因为M=13，所以n=4。

状态编码：取自然二进制数的0000～1100作为S₀～S₁₂的编码，如下表所示。

表 电路的状态转换表

画出表示次态逻辑函数和进位输出函数的卡诺图，如图5.7所示。

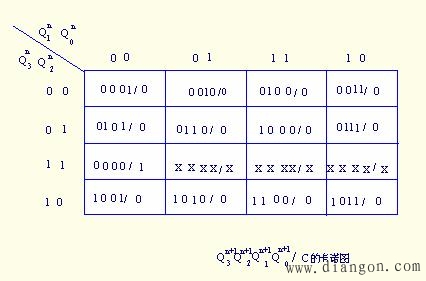
图5.7 例5.3的卡诺图

为清晰起见，可将上图的卡诺图分解为五个卡诺图，如图5.8所示。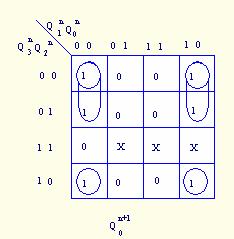

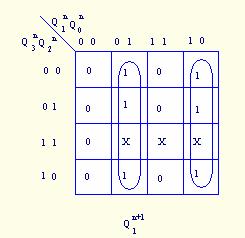
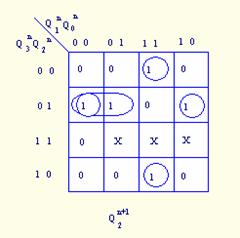
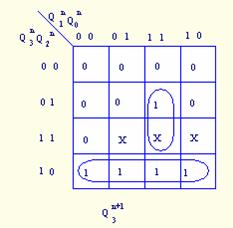
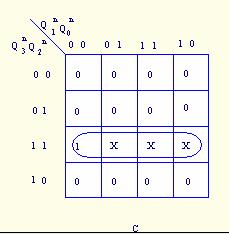
图5.8 的卡诺图

从卡诺图得电路的状态方程为:

输出方程为 : C=Q₃Q₂

如果选用JK触发器，把状态方程进行变换，得驱动方程：

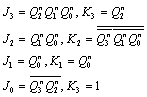
画出计数器的逻辑图如图5.9所示。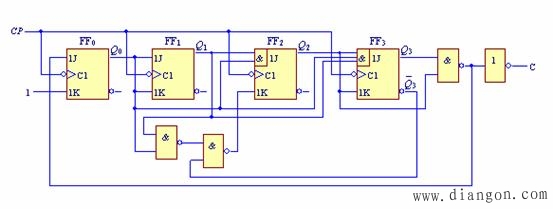

图5.9 例5.3的电路

检查电路能否自启动。将三个无效状态1101、1110、1111分别代入电路中进行分析，所得次态分别为0010、0010、0000，因此电路能自启动。

下图是该电路完整的状态转换图。

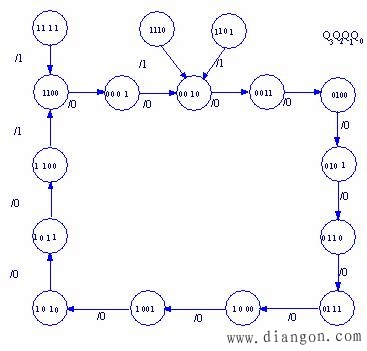
图5.10 例5.3的状态转换图

例5.4 设计一个串行数据检测器。对它的要求是：连续输入3个或3个以上的1时输出为1，其他输入情况下输出为0。

解：首先进行逻辑抽象，画出状态转换图。

取输入数据为输入变量，用X表示；取检测结果为输出变量，用Y表示。

设S₀：没有输入1以前的状态，

S₁：输入一个1以后的状态，

S₂：输入两个1以后的状态

S₃：输入3个或3个以上1以后的状态。

若以Sⁿ表示电路的现态，Sⁿ⁺¹表示电路的次态，可得状态转换表，如表所示。

表 状态转换表

Sⁿ⁺¹/Y

状态转换图如图5.11所示。

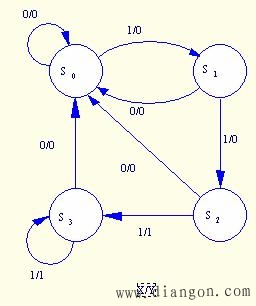
图5.11 例5.4状态转换图

进行状态简化。S₂和S₃是等价状态，可以合并为一个。于是得到化简后的状态转换图。

在电路状态M=3的情况下，取触发器位数 n = 2.

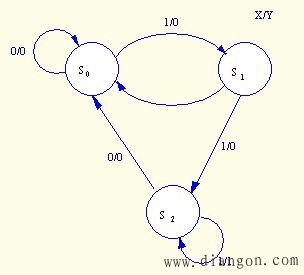
图5.12 例5.4化简后的状态转换图

取S₀=00，S₁=01，S₂=10，选定JK触发器，得次态和输出的卡诺图，如图5.13所示。

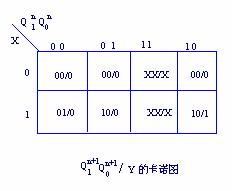
图5.13 例5.4的电路次态/输出卡诺图

经化简得状态方程为:

得驱动方程为

输出方程为 : Y=XQ₁

由驱动方程和输出方程得电路图如图5.14所示。

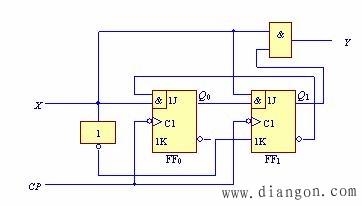
图5.14 例5.4的电路

电路状态转换图如图5.15所示。

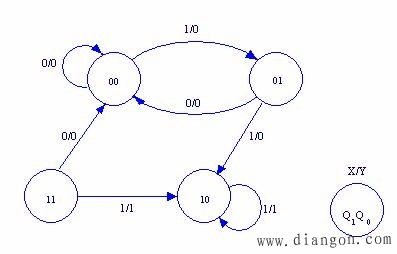
图5.15 例5.4的状态转换图

这个电路能够自启动。

若改用D触发器，则驱动方程为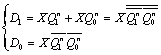

得电路图如图5.16所示.

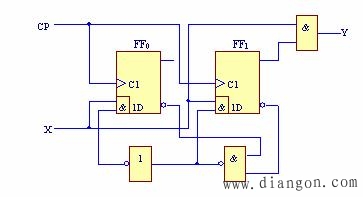
图5.16