一、线形电阻元件
1．线性定常电阻元件 若电阻元件的伏安关系是通过u-i（或i-u)平面上坐标原点的直线，且此直线的位置（亦即直线的斜率）不随时间变动，则称为线性定常电阻元件时不变电阻元件。，如图1（a）所示， 它有如下特点：
（1）.直线的斜率即为其电阻值R，即tg(α)=R,且R值为定值（即不随时间而变）。这样即可用一个定常电阻R或定常电导G来构成线形定常电阻元件的电路模型，如图1（b）所示，且有G=1/R或R=1/G。
（2）.伏安关系曲线对坐标原点对称，即为奇函数。这说明线形定常电阻元件对不同方向的电流或不同极性的电压，其伏安关系是完全相同的。这种性质称为双向性，也称可逆性。因此在使用线形定常电阻元件时，它的两个端纽是没有任何区别的，在电路中可以任意连接。
（3）.它的伏安关系服从欧姆定律。若设电压u与电流i之间参考方向如图1（b）所示，则有
u=Ri （1-3-1a）
或 i=
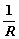u=Gu (1-3-1b)上式即为欧姆定律，它说明电阻元件的电流或电压，完全由同一时刻的电压（或电流）决定，而与该时刻以前的电压（或电流）值无关，即电阻元件是无记忆元件。
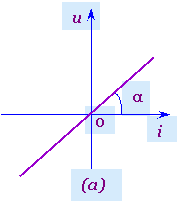
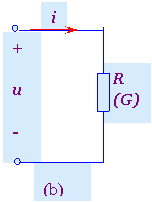
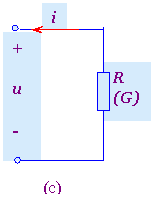
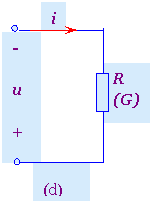
图1 线性定常电阻元件
2.线性时变电阻元件若电阻元件的伏安关系曲线是通过u-i平面上坐标原点的直线，但此直线的斜率是时间t的函数（即其电阻随时间t而变化），则称为线性时变电阻元件。 如图2(a)所示，其电路模型如图2(b)所示，其伏安方程为
u=R(t)i 或 i=G(t)u
式中 R(t)和G(t)分别为电阻元件在t时刻的电阻值和电导值，且有R(t)=1/G(t)或G(t)=1/R(t);R(t)为t时刻的斜率。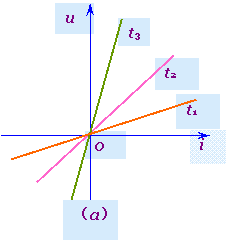
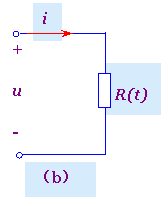
图2 线性时变电阻元件
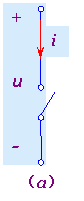
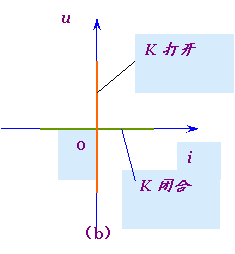
图3 理想开关及其伏安特性
线性时变电阻的一个常见实例是理想开关K，它的电路符号如图3（a）所示。当K打开时，它的伏安关系为电流i恒为0，u=不定值（其值由开关以外的电路工作状态决定），其伏安关系曲线为u-i平面上的u轴，如图3（b）所示，相应于电阻值R=∞；
当K闭合时，其伏安关系为电压u恒为0，i=不定值（其值由开关以外的电路工作状态决定），其伏安关系曲线为u-i平面上的i轴，如图3（b）所示，相应于电阻值R=0。
二、非线性电阻元件
1．非线性定常电阻元件 若电阻元件的伏安关系曲线不是通过u-i平面上坐标原点的直线而是曲线，且此曲线的位置不随时间t而变动，则称为非线性定常电阻元件或非线性时不变电阻元件。 它不服从欧姆定律，且一般不具有双向性。如图4（a）所示。
2．非线性时变电阻元件 若电阻元件的伏安关系曲线是通过u-i平面上坐标原点的曲线，且曲线的位置随时间t而变动，则称为非线性时变电阻元件。
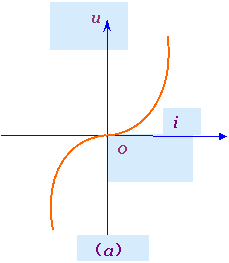
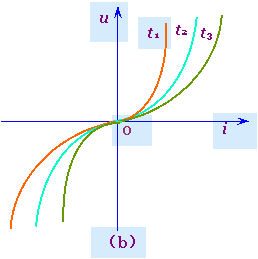
图4 非线性电阻元件