图1(a)所示的电路的节点N与q之间有一理想电压源us。今将该理想电压源分裂成三个(即等于与N点相联的其余支路的个数)理想电压源的并联,其电压均为us,如图1(b)所示。这并不改变电路中各节点间的电压关系,故图(b)与图(a)是等效的。图(a)中的一个节点N在图(b)中分裂成了N1、N2及N3三个点,但这三个点仍然连在一起,它们的电位相同。今将图(b)中的联线N1-N2、N2-N3断开,即成为图(c)电路。图(c)中N1、N2、N3三个点的电位仍相同。由于图(c)中的电压uaq、ubq、ucq与图(a)中的相应电压完全相同,对电流i1、i2、i3无任何影响,故图(c)与图(a)也是等效的。进而再将图(c)依次改画成图(d)、(e)、(f),则图(f)与图(a)也等效。将图(a)等效变换成图(f)即称为理想电压源的等效分裂。在图(f)中,每一个理想电压源与一个对应的电阻串联,即构成一个有伴电压源电路。既然可以将图(a)等效变换成图(f),当然也可以反过来将图(f)等效变换为(a)。这种相反的等效变换称为理想电压源的等效合并。
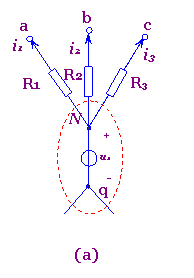
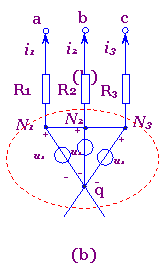
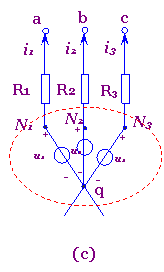
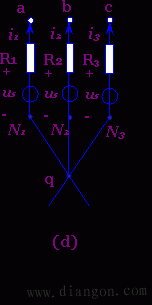
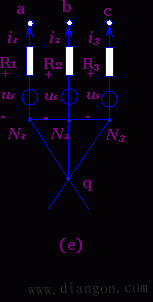
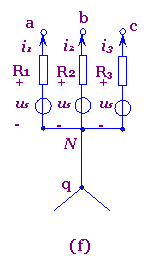
图1 理想电压源的等效分裂与合并
二.理想电流源的等效分裂与合并
图2(a)所示电路中的节点a与d间接有一理想电流源is,今将该理想电流源分裂成三个(即等于abcd回路中其余支路的个数)电流源的串联,其电流均为is,如图2(b)所示.这并不改变电路中各支路电流的关系,所以图(b)与图(a)是等效的.由于电流源分裂后在图(b)中多了两个节点b’ ,c’上分别应用KCL,立即可知联接线b'b与c’c中的电流为零.这说明联接线b’b与c’c的加入对电路中各支路电流的关系毫无影响.因此图(c)与图(a)也是等效的.将图(c)再画成图(d)所示电路.电路的这种等效变换称为理想电流源的等效分裂.同样可以反过来将图(d)等效变换为图(a).这种相反的等效变换称为理想电流源的等效合并.
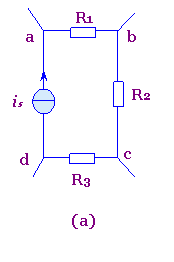
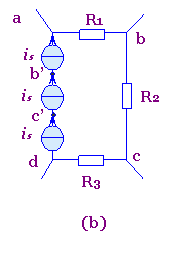
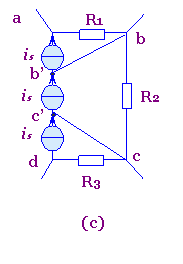
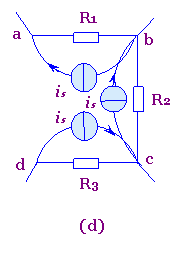
图2 理想电流源的等效分裂与合并
