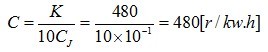一、圆盘的转动定性分析
1、磁通的分布情况：
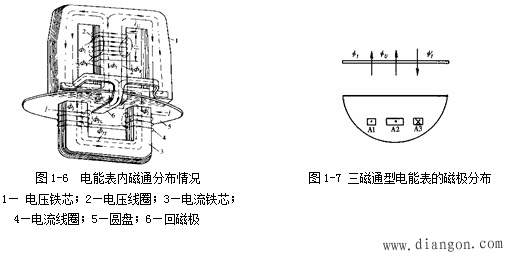
由右手螺旋定则，交变电流经过导线或线圈时，会产生磁场。如图1-6所示电线圈并联在电源两端，电压U在电压线圈中产生激磁电流IU, IU产生的磁通ΦU从电压铁芯中柱经磁极穿过圆盘回中柱,叫电压工作磁通。电流元件位于圆盘下方，电流线圈串联在电路和负载之间，负载电流I产生的电流工作磁通ΦI，Φ´I穿过原盘。因此，对圆盘而言，有两个大小相等、方向相反的两束电流工作磁通ΦI，Φ´I从不同位置两次穿过圆盘，而电压工作磁通ΦU一次穿过圆盘，于是相当于有三束磁通作用于圆盘上，所以，我们把感应式电能友又称为“三磁通型”电能表。
“三磁通型”电能表。如图1-7所示。现规定：磁通从下往上通过转盘为N极，以“．”表示，磁通从上往下通过转盘为s极，以“× ”表示，所以转盘上三个磁极的位置分别为A1(N极)、A2(N极)、A3(s极)。
2、驱动力矩的产生
因电压铁芯和电流铁芯都不闭合，有气隙，所以在磁路不饱和段可看成线性铁芯，当激磁电流I 和 IU为正弦波时，其产生的响应磁通也为正弦波。三束交变的磁通作用在圆盘上，根据电磁感应定律，就会在圆盘内产生三个交变的感应电流，且相位滞后于对应的磁通90º。这三个感应电流也叫涡流，其波形仍是正弦波。根据左手定则可知，三个工作磁通ΦI，Φ´I 和ΦU分别与穿过各自区域的涡流相互作用，产生推动圆盘转动的电磁力。其作用对应关系如图1-8所示（见图1-8 （ab）电磁力的产生和图1-8 （cd）电磁力的产生）。
由于磁通ΦI，Φ´I 和ΦU随时间按正弦规律变化，所以当磁通穿过转盘时，在转盘上呈现的磁极极性及磁通量的大小也是变化的。对时间t1至t4瞬时来说，穿过转盘磁通最大值从磁极A1向磁极A3逐渐移动，也就是说，在一个周期内，它经过了所有3个磁极，我们可看作有个磁场不断重复地从磁极A1移向A3，这就是旋转磁场。即旋转磁场的方向是从相位超前的磁通所在的空间位量（ΦI）移向相位迟后的磁通(ΦU)所在的空间位置。按图示的磁极位置中旋转磁场的方向为逆时针移动方向，如果改变磁通ΦI和ΦU的相位关系，便可以改变旋转磁场的方向。
总的来说，转动力矩由两部分所组成：电压磁通由ΦU与电流磁通所产生的涡流iPI 、 i′PI ，相互作用而产生F1、F2；电流磁通ΦI，Φ′I与电压磁通所产生的涡流iPU相互作用所产生F3、F4。我们可以分四个区域来研究电能表力矩的产生 。如图1-8所示。
1）、0~1/8 T时间电磁力的方向分析
（1）由图1-6得穿过转盘的磁通ΦU 、 ΦI，Φ′I方向。
（2）由课本图1-8得该时间段内各磁通的变化趋势。
（3）根据楞次定理和右手定则得涡流iPU、iPI 、 i′PI的方向。
（4）由左手定则判断各电磁力的方向。
2）、同理可分析其他时段电磁力的方向分析
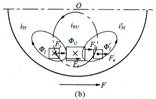
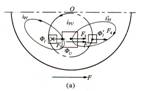
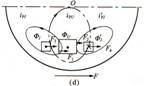
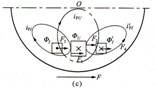图1-8电磁力的方向分析a）0~1/8 T时间；b）t=(2/8)T~(3/8)T；c）t=(4/8)T~(5/8)T；d）t=(6/8)T~(7/8)T
3）、t=tx时电磁力的方向分析
根据左手定则判定电磁力F1、F2方向向左，F3、F4的方向向右，这时，转盘的转动方向由多数时刻电磁力的方向决定，且，其转动有惯性。所以，在一个周期T内，转盘始终逆时针方向转动。 （3）圆盘转数与被测电能的关系：电能表常
由上述条件，当负载功率不变时，驱动力矩与制动力矩保持平衡，于是圆盘便作勾速转动。当负载功率增加或减少时，驱动力矩便随之增加或减少，于是圆盘转速也随之变快或变侵。所以，制动力矩MT也要增加或减少，直到负载功率不再改变时，驱动力矩又在新的条件下与制动力矩保持平衡。于是圆盘便在新的转速下作匀速转动。总之，制动力矩总是能够与驱动力矩保持平衡。所以，当圆盘作匀速转动时必有下列关系：
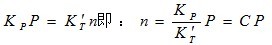（1-7）
假定某一段时间内负载功率保持不变，并设时间T内圆盘转过N转，则N＝nT。代入式（1-7），则有：
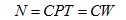（1-8）
式中 W—时间T内通过电能表的电量，kw•h；C—电能表的常数，r/(kw•h)。
式(1—8)说明，电能表在一定的功率下运行，经过时间T圆盘转过的转数是与这段时间内通过电能表的电量成正比的，因此通过记录转盘转数的计度器，可以显示出负载在一定时间内所消耗的电能。所以，可以用圆盘转数代表电量的多少，并且，它对变化的负载也是适用的。
5、计度器示数与被测电能的关系：
电能最终要通过计度器直接显示出来，则还需计度器的齿轮能将回盘的转数转换为以电能为单位的指示值。它们之间的关系可用下面的公式表示：
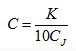（1-9）
式中， K—传动比，它是末位字轮走一整圈，转盘转动的圈数。
CJ—计度器的系数，kw•h/字。末位字轮走一个字代表的千瓦小时数。
为了方便电量的抄读。取CJ为10的整数次幂，则CJ＝10a，显然a由计度器窗口的小数值决定。当小数位窗口为一位时，a=-1，小数窗口为两位时，a＝-2以此类推，当末位窗口为整数位时，a＝0。末位字轮转一周是10个字，因此，10CJ是末位字轮转一周所代表的千瓦小时数。二者之间的比值恰符合电能表常数的定义，即每千瓦小时圆盘的转数。
举例说明，例1-1：
某感应式电能表计度器传动比K＝480r，其窗口有一位小数位。求该电能表常数应为多少?
解：窗口有一位小数位，即CJ＝10-1 kw•h/字。
该电能表常数：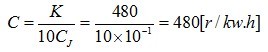
（3）圆盘转数与被测电能的关系：电能表常
由上述条件，当负载功率不变时，驱动力矩与制动力矩保持平衡，于是圆盘便作勾速转动。当负载功率增加或减少时，驱动力矩便随之增加或减少，于是圆盘转速也随之变快或变侵。所以，制动力矩MT也要增加或减少，直到负载功率不再改变时，驱动力矩又在新的条件下与制动力矩保持平衡。于是圆盘便在新的转速下作匀速转动。总之，制动力矩总是能够与驱动力矩保持平衡。所以，当圆盘作匀速转动时必有下列关系：
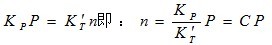（1-7）
假定某一段时间内负载功率保持不变，并设时间T内圆盘转过N转，则N＝nT。代入式（1-7），则有：
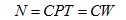（1-8）
式中 W—时间T内通过电能表的电量，kw•h；C—电能表的常数，r/(kw•h)。
式(1—8)说明，电能表在一定的功率下运行，经过时间T圆盘转过的转数是与这段时间内通过电能表的电量成正比的，因此通过记录转盘转数的计度器，可以显示出负载在一定时间内所消耗的电能。所以，可以用圆盘转数代表电量的多少，并且，它对变化的负载也是适用的。
5、计度器示数与被测电能的关系：
电能最终要通过计度器直接显示出来，则还需计度器的齿轮能将回盘的转数转换为以电能为单位的指示值。它们之间的关系可用下面的公式表示：
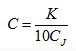（1-9）
式中， K—传动比，它是末位字轮走一整圈，转盘转动的圈数。
CJ—计度器的系数，kw•h/字。末位字轮走一个字代表的千瓦小时数。
为了方便电量的抄读。取CJ为10的整数次幂，则CJ＝10a，显然a由计度器窗口的小数值决定。当小数位窗口为一位时，a=-1，小数窗口为两位时，a＝-2以此类推，当末位窗口为整数位时，a＝0。末位字轮转一周是10个字，因此，10CJ是末位字轮转一周所代表的千瓦小时数。二者之间的比值恰符合电能表常数的定义，即每千瓦小时圆盘的转数。
举例说明，例1-1：
某感应式电能表计度器传动比K＝480r，其窗口有一位小数位。求该电能表常数应为多少?
解：窗口有一位小数位，即CJ＝10-1 kw•h/字。
该电能表常数：