 |
|---|
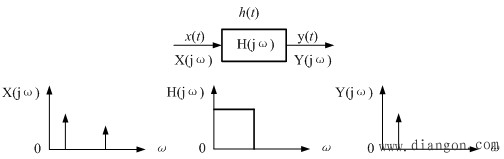
| 1.描述滤波器的动态特性的有3种形式: |
| (1)单位冲激响应: |
| x(t)=δ(t),y(t)=h(t) |
| (2)传递函数 |
|
|
| (3)频率特性 |
|
|
| 2.滤波器的种类 |
| 有源滤波器按幅频特性可分为低通、高通、带通和带阻4种类型。 |
 |
| (1)低通滤波器(lowpass filter):低于截止频率fc的频率可以通过,高频率成份被滤掉。 |
| (2)高通滤波器(highpass filter):高于截止频率fc的频率可以通过,低频成份被滤掉。 |
| (3)带通滤波器(bandpass filter):只有高于fL低于fH的频率可以通过,其它成份均被滤掉。 |
| (4)带阻滤波器(bandreject filter):在fL与fH之间的频率被滤掉,其它成份均可以通过。作为特例,只有特定频率成分可以通过的滤波器被称为陷波滤波器(notch filter)。 |
| 类 型 | 传 递 函 数 | 性 能 参 数 |
| 低通 |
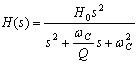 |
H0:任意增益因子 ? wC:低通、高通滤波器截止角频率 ? w0 :带通、带阻中心频率 Q:品质因素 |
| 高通 |
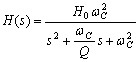 | |
| 带通 |
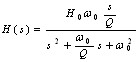 | |
| 带阻 |
 |
| 3.滤波器的阶数和特性 |
| 巴特沃思: 通带内幅频曲线的幅度平坦,最平幅度逼近,相移与频率的关系不是很线性的,阶跃响应有过冲。 |
| 切比雪夫: 下降最陡,但通带之间幅频曲线有波纹。 |
| 贝塞尔:相移和频率之间有良好的线性关系,阶跃响应过冲小,但幅频曲线的下降陡度较差。 |
 |
| 4.滤波器的电路结构 |
| 无限增益多重反馈滤波器电路 |
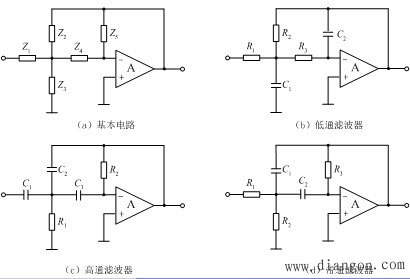 |
| 电压控制电压源(VCVS)电路 |
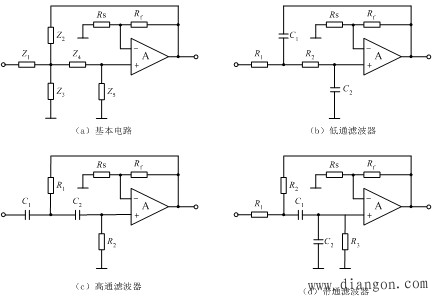 |
| 典型滤波器的设计 |
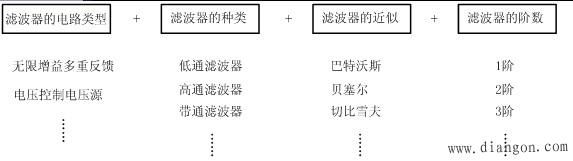 |
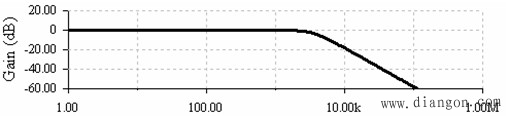
| 例2.1-1 二阶无限增益多重反馈低通滤波器的设计。假设滤波器的通带增益A0=1,截止频率fC=3.4kHz,Q为0.707。 |
| 电路结构 |
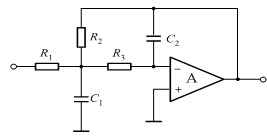 |
| 传递函数 |
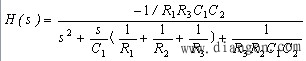 |
| 解: |
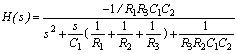 与 与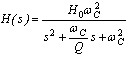 比较 比较 |
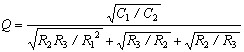 |
|
令C1=nC2 ,A0= |
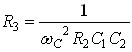 代入Q的表达式 代入Q的表达式 |
得: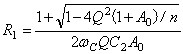 |
| 取n=4Q2(1+A0),上式可进一步简化为: |
|
|
| 令 |
| C1=4Q2(1+A0)C2 |
| R1=R0/(2Q A0) |
| R2= A0×R1 |
| R3= R0/[2Q (1+A0)] |
| 由此可见,只要确定C2的值,其余的参数可随之确定。 |
| (1)首先决定C2的容量,再根据电容容量,用R0=1/2πfCC2公式计算基准电阻R0。选取C2值为2200pF,则基准电阻R0=1/2πfCC2=21.29kΩ。 |
| (2)计算C1的电容值,C1=4Q2(1+A0)C0=8797 pF |
| (3)计算R1的电阻值,R1=R0/(2Q A0)=15.05 kΩ |
| (4)计算R2的电阻值,R2= A0×R1=15.05 kΩ |
| (5)计算R3的电阻值,R3= R0/[2Q (1+A0)]=7.53 kΩ |
| 各电阻、电容取标称值以后滤波器原理图 |
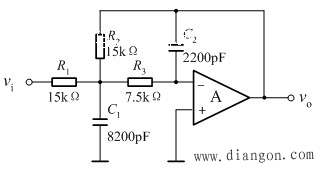 |
| 二阶低通滤波器幅频特性仿真结果 |
 |
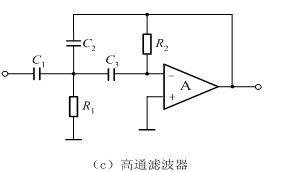
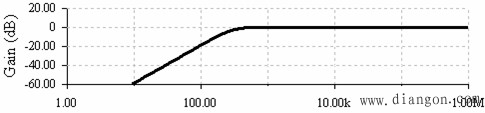
| 例2.1-2 二阶无限增益多重反馈高通滤波器的设计。设滤波器通带增益A0=1,截止频率fc=300Hz,Q为0.707。 |
 |
| 解:取基准电容C0=0.033uF,则基准电阻R0=1/(2πfcC0)=16.076KΩ, |
| C1=C2=C0=1/(2πfcR0)=0.033uF |
| C3= C0/A0=0.033uF |
| R1=R0/[Q(2+1/A0)]=7.58 KΩ |
| R2=R0Q(1+2A0)]=34.097KΩ |
| 各电阻、电容取标称值以后滤波器原理图 |
 |
| 二阶高通滤波器幅频特性仿真结果 |
 |
