
| 模拟电子系统就是典型的连续时间系统。 |
| 数字电子系统就是典型的离散时间系统。 |
| 抽样数据处理系统 |
| 连续信号在离散瞬时间nT(n=0,1,2,…)下抽样就得到抽样数据信号,用x=(nT)表示,T为抽样周期。 |
| 抽样数据处理系统:处理抽样数据信号的系统称为抽样数据处理系统。 |
| 抽样数据输入和输出信号通常表示成离散变量nT的函数。 |
| x=x(nT),y=y(nT) |
| 抽样数据信号只在离散瞬时改变,因此,属于离散时间系统。 |
| 抽样数据电路 |
| 抽样数据电路处理的是抽样信号,即时间离散而幅度连续的信号,它是一种离散时间电路,所以其基本单元与数字电路类似,但因它所处理的信号没有量化,所以不会产生量化噪声。 |
| 抽样数据电路主要有三种类型: | |
| 电荷耦合器件(CCD,Charge Coupled Device) | |
| 开关电容电路(SC,Switched Capacitor Circuits) | |
| 开关电流电路(SI,Switched Current Circuits) | |
| 开关电容电路 | |
 |
 |
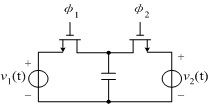
| 开关电容由两个MOS开关和MOS电容组成。 | |
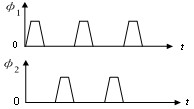
| Φ1和Φ1是不重叠的两相时钟脉冲,因此两只MOS管轮流导通。 | |
| 用开关电容来模仿电阻 |
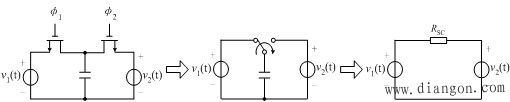 |
| 开关电容相当于一个电阻 |
| 原理分析 : |
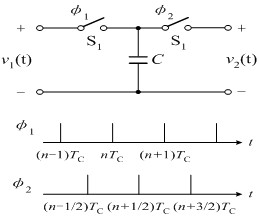 |
| 在t=(n-1)TC时刻,开关打在左边,电容充电至v1(t),其充电量为 |
| qC(t)=C v1 [(n-1)TC] |
| 在(n-1/2)TC时刻,开关打在右边,电容放电至v2(t),电容上电量为 |
| qC(t)=qC [(n-1/2)TC]=C v2 [(n-1/ 2)TC] |
| 在每一个时钟周期TC内,电容上电荷的变化量为 |
|
|
| 从近似平均的角度看,可以把一个TC内由v1(t)送往v2(t)的ΔqC(t)等效为一个平均电流iC(t),其大小为: |
|
|
| 因为时钟脉冲周期TC远远小于v1(t)和v2(t)的周期,故在TC内可认为v1(t)和2(t)v2(t)是恒值。 |
|
|
|
|
| 开关电容能模拟成电阻,解决了模拟集成电路制造中的一个关键问题。因为在集成电路制造过程中,电阻常常受到容差和热漂移所困扰,而且要占据昂贵的芯片面积。 |
| 例如,制造一个10MΩ的集成电阻所占硅片衬底面积约为1mm2,而制造一个10MΩ的开关电容模拟电阻,在fC=100kHz时,只要制造1pF的MOS电容,该电容占用的硅片衬底面积只有0.01 mm2。 |
| 开关电容积分器 | |
| 模拟积分器 | |
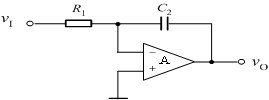 | |
|
| |
|
|
|
| 用开关电容代替积分器中的电阻 | |
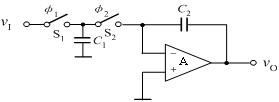 | |
| 当ωC>>ω时,由vI流向求和节点的电流就可以认为是连续的。 | |
|
| |
| 结论: |
| 电路中没有电阻。 |
| 特征频率ω0取决于电容比值,采用现有的技术,很容易就可以达到低至0.1%的比值容差。 |
| 特征频率ω0与时钟频率fc成比例,表明开关电容必然是可编程的。改变会在频谱图上使响应上移或下移。另一方面,如果需要一个固定和稳定的特征频率fC ,则可用一石英晶体振荡器来产生fC。 |
| 有源双二阶滤波器 |
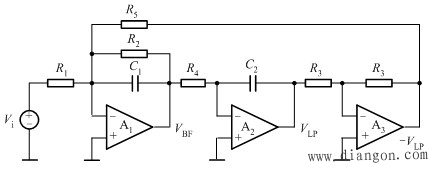 |
| SC双二阶滤波器 |
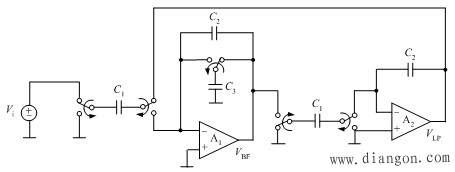 |
| 单片集成滤波器 |
| 单片集成滤波器大都是SCF。原因是它的时间常数取决于电容化集成工艺,可实现高精度和高稳定度的电容比。 |
| 单片集成SCF较具代表性的产品主要有美国Linear Technology(凌特)公司生产的通用型(可组合为低通、带通、高通等)和低通SCF两类。通用型SCF主要有:LTC1059(2阶)、LTC1060(4阶)、LTC1061(6阶)、LTC1064(8阶)等。低通SCF主要有:LTC1062/1063(5阶)、LTC1064(8阶)。 |
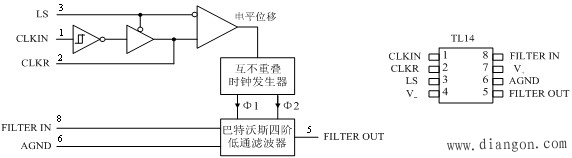
| TL14——巴特沃斯四阶低通开关电容滤波器 |
| (1)低成本、易用; |
| (2)滤波器的截止频率取决于外部时钟频率; |
| (3)截止频率范围从0.1Hz至30kHz。 |
 |
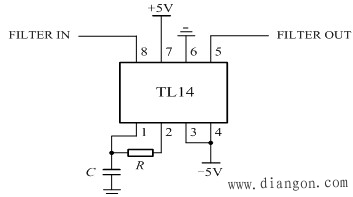 |
| fc= fCLOCK /100 |
