动态电路的初始条件

在动态电路中，电感电流和电容电压分别与电感和电容的储能直接相关，它们共同反映电路的能量状态，通常所说电路的状态，就是通过,来表达的。

动态电路的动力学过程，任一时刻都应毫无例外地遵循基尔霍夫定律和元件上的电压电流关系，即电路方程；此时，这些方程将是微分方程。如果元件都是线性的，而且其参数R，L,C又都是常量，则电路方程将是线性常系数微分方程。本章研究动态电路的过渡过程是以时间为自变量，在时间域内进行的，故称为时域分析。

为了求解微分方程，我们首先要关注电路状态参变量电流与电压的初始值。电路条件的突然变更，诸如开关动作、参数及电源的变动等都将使电路的状态出现新的变动，称之为电路发生换路。工程上常把出现这种新过程的瞬间称为初始时刻，此刻电路的状态，就是初始状态。从电路的微分方程来看，就是初始条件。

根据第二章的讨论，在换路瞬间，当电路中电容的电流为有限值和电感两端的电压为有限值时，电容上的电压和电感中的电流保持连续，即不发生突变，这一规律称为换路定则。

换路定则一般可表达为

(5.<?xml:namespace prefix = st1 />1.1a)

(5.1.1b)

由于磁通和电荷量，故上述条件也可改写为

(5.1.2a)

(5.1.2b)

由此可见：电路中有几个独立的动态元件（即L、C），便可利用（5.1.1）式或（5.1.2）式决定几个初始值，并且通过它们来确定电路微分方程通解中的积分常数。

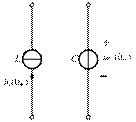
(a) 稳态时的L和C (b) 换路前有储能的L和C (c) 换路前无储能的L和C

图5.1.1 电容与电感在稳态和换路后的等效模型

动态电路中电流与电压初始值的求法和步骤如下。

1. 求出时，电感电流与电容电压的值

画出换路前终了时刻的电路。对于直流电路，当电路已处稳态（，）时，根据图5.1.1(a)，则电容可用开路替代，电感用短路替代；独立源、电阻、受控源保持不变，得到时刻的等效电路——特殊的电阻电路。由此电路求出和。对于正弦交流电路，则是用相量法求出换路前正弦稳态电路的电容电压相量和电感电流相量，然后把电容电压相量和电感电压相量还原成时间函数和，代入，求出和。

2. 求时，电感电流与电容电压的值

由(5.1.1)的换路定则，求出电感电流与电容电压在的值，即

，

3. 初始值的确定

（1）画出换路后初始时刻的电路，电容用电压为的电压源替代；电感用电流的电流源替代；受控源和电阻不变；独立电压源和电流源的电压和电流取其在时的值，电源性质不变。由此得到时刻的等效电路——特殊的电阻电路。

（2）在等效电路中，应用KCL,KVL和欧姆定律等电阻电路的求解方法，即可求出等物理量的初始值。