对于一个电路图,如果用点表示其节点,用线段表示其支路,得到一个由点和线段组成的图,这个图被称为对应电路图的拓扑图,通常用符号G表示。例如:图1(a)所示电路,其对应的拓扑图如图1 (b) 所示。
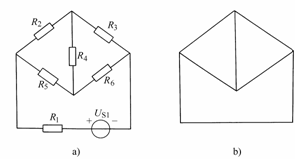
图1
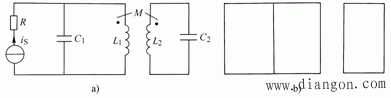
图2
拓扑图是线段和点组成的集合,它反映了对应的电路图中的支路数、节点数以及各支路与节点之间相互连接的信息。
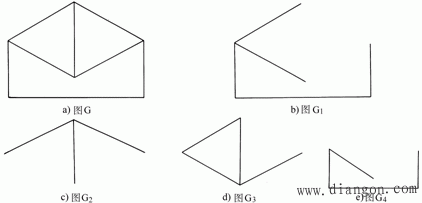
图3
在拓扑图中,如果任意两点之间至少有一条连通的途径,那么这样的图称为连通图,例如图1(b)所示的图,否则称为非连通图,例如图2(b)所示的图。如果图G1中所有的线段与点均是图G中的全部或部分线段与点,且线段与点的连接关系与图G中的一致,那么图G1称为图G的子图。例如图(b)(c)(d)(e)均是图3(a)的子图。
下面介绍网络图论中非常重要的一个概念——树。树是连通图G的一个特殊子图,必须同时满足以下三个条件:
(1)子图本身是连通的;
(2)包括连通图G所有节点;
(3)不包含任意回路。
组成树的支路称为树支,不包含在树上的支路称为连支(或链支)。如果用![]() 表示树支的数目,则:
表示树支的数目,则:![]() (式1)
(式1)
连支的数目![]() 等于支路数b减去树支的数目,即:
等于支路数b减去树支的数目,即:![]() (式2)
(式2)
如果将一个电路铺在一个平面上,除节点之外再没有其他交点,这样的电路被称为平面电路,否则,称为非平面电路。
在平面电路中,内部没有任何支路的回路称为网孔。它是一种特殊的回路。
一个有b条支路、n个节点的连通平面图的网孔数m为:![]() (式3)
(式3)
接下来介绍割集的概念。割集是连通图G的一个子图,它满足以下两个条件:
(1)移去该子图的全部支路,连通图G将被分为两个独立部分;
(2)当少移去该子图中任一条支路时,则图仍然保持连通。
一个具有n个节点的连通图,有(n-1)条树,有(n-1)个单树支割集。
