三相制供电是电力系统普遍采用的供电方式，所谓三相制就是由三个频率相同、相位不同的电源作为供电体系。三相制之所以获得广泛应用，主要是因为它在发电、输送和负载驱动方面与单相制相比有许多优点。与三相供电电源相对应，每组负载也由三个组成，称为三相负载。
三相电源的三个电势和三相负载阻抗有两种基本连接方式，即星形联结（Y联结）和三角形联结（△联结）。图1分别示出了三相电源与三相负载的Y联结与△联结。每相电源
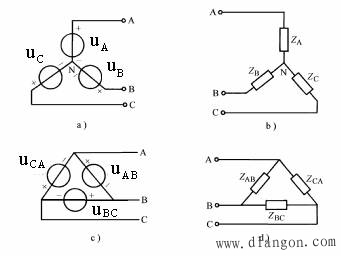
图1
与负载分别标以A相、B相和C相加以区别。在Y联结方法中，各相电源和负载的输出端称为各相的端点，三相公共联结点称为中性点，或简称为中点。在△联结方法中，三相电源或负载分别首尾相连，无中性点。由三相电源或三相负载连接而成的电路称为三相电路。
图2画出了电源和负载均为星形联结的三相电路图。图中Zl表示每相线路阻抗，从电源端点A、B、C至负载端点
、
、
的三根连线称为端线，通常称为火线。Y形联结的三相电源的中点N与负载中点
的连结称为中性线或中线。在三相星形联结中，具有三根端线和一根中性线的供电方式称为三相四线制，没有中性线的供电方式称为三相三线制。
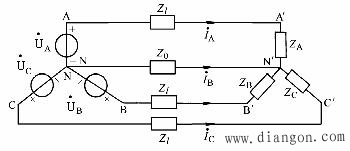
图2
图3分别表示了Y形联结电源与△形联结负载，以及△形联结电源与△形联结负载的连线方式。在这些联结方式中，对于三相电源和三相负载，不论是△形还是Y形接法，规定通过每个电压源或每个负载阻抗的电流称为相电流，每个电压源或负载阻抗两端的电压称为相电压。流过三根端线的电流称为线电流，端线与端线之间的电压称为线电压。
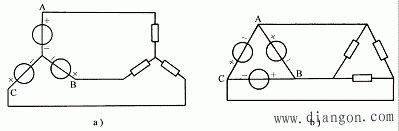
图3
如果在三相电源中，三个正弦电压源的振幅相等，电压源之间的相位差均为1/3周期（
），则称这种三相电源系统为对称三相电源。以图2所Y形联结的三相电源系统为例，设各相电动势分别为
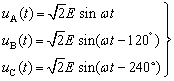（1）
则它为对称三相电源，可用相量表示为
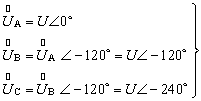（2）
对称三相电源的波形图和相量图分别示于图4中。对于△形联结的三相电源，从波形图可见由于三相电动势串联后
，因此在△形闭合回路中不会产生环流。
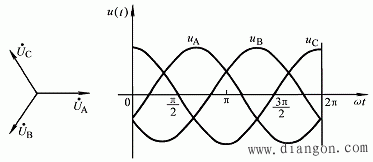
图4
首先分析Y形联结的对称三相负载的线电压、线电流与相电压、相电流之间的关系。图5所示为一Y形联结的对称三相负载，设负载的各相电压为对称且为正序，则电压相量可表示为
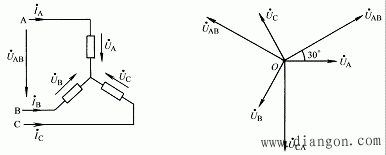
图5
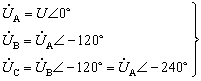（3）
线电压为：
（
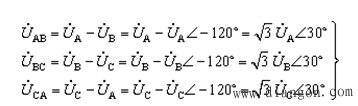对称三相Y形联结的负载电路，其线电压也是一组对称的三相电压，线电压有效值是相电压有效值的
倍，
相位超前
角。电压相量图如图4-3-5所示。通过负载各相的电流为：
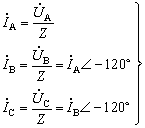（5）
可见负载各相电流也是一组对称三相电流，相序与电压相同。对于Y形联结而言，相电流等于线电流。
对于△形联结的对称三相负载，如图6所示，各相电压即等于对应端线间的线电压，如果线电压为对称三相电压，即有：
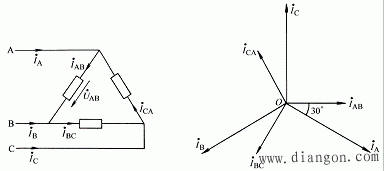
图6
则负载相电流为一组对称三相电流。
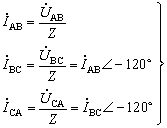（6）
根据基尔霍夫节点电流定律，可求得线电流为
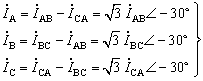（7）
可见线电流也为一组对称三相电流，线电流
滞后相电流
，其有效值为相电流的倍。电流相量见图6b。
下面分析对称三相电路的计算特点。图7为三相四线制电路，由三相对称电源和三相对称负载组成，Zl为线路阻抗，Z0为中线阻抗。设中点N为参考，则可求得：
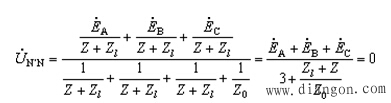
可见对称三相电路中性点的电位是相等的。各相电流：
中线电流
。因为对称三相负载的阻抗相等，可知相电压为一组对称三相电压。
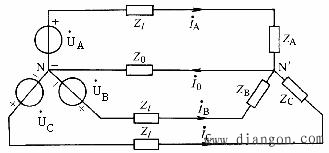
图7
例1 图8a为由两组对称三相电源供电的三相电路。已知
，
，
，
，
，试求负载
上的相电压与相电流。
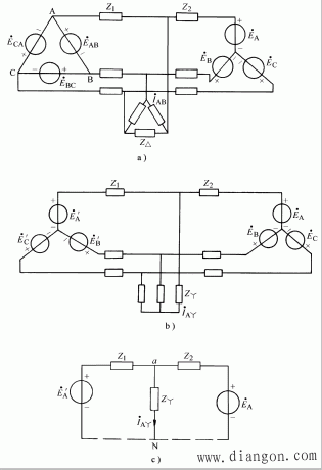
图8
解：为画出单相图，需将△形联结的电源与△形联结的负载转换为Y形联结，如图8b。
由△－Y转换的相电压线电压关系，可知△形联结的电源等效转换为Y形联结的相电势为：
由△形联结负载转换为Y形联结后其等效阻抗为：
即 ： 
取A相电路，并把各中性点联结，则得到如图4-3-8c所示的单相图。设N为参考点，则列节点方程为：
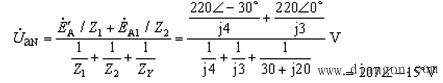
则： 
此为Y形联结的相电流，也为线电流值。则△形联结的实际相电流为
相电压为： 
由对称性可写出各相电压电流值为
，
，
，
，
