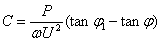直流电路的功率等于电流与电压的乘积，但交流电路则不然。在计算交流电路的平均功率时还要考虑电压与电流间的相位差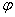
，即
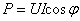
上式中的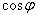
是电路的功率因数。电压与电流间的相位差或电路的功率因数决定于电路(负载)的参数。只有在电阻负载(例如白炽灯、电阻炉等)的情况下，电压和电流才同相，其功率因数为1。对其他负载来说，其功率因数均介于0与1之间。
当电压与电流之间有相位差时，即功率因数不等于1时，电路中发生能量互换，出现无功功率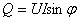
。这样就引起下面两个问题：
(1) 发电设备的容量不能充分利用
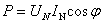
由上式可见，当负载的功率因数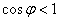
时，而发电机的电压和电流又不容许超过额定值，显然这时发电机所能发出的有功功率就减小了。功率因数愈低，发电机所发出的有功功率就愈小，而无功功率却愈大。无功功率愈大，即电路中能量互换的规模愈大，则发电机发出的能量就不能充分利用，其中有一部分即在发电机与负载之间进行互换。
例如容量为1000kV/A的变容器，如果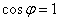
，即能发出1000kW的有功功率，而在
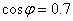时，则只能发出700kW的功率。
(2) 增加线路和发电机绕组的功率损耗
当发电机的电压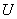
和输出的功率
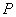一定时，电流
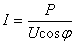与功率因数成反比，而线路和发电机绕组上的功率损耗
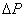则与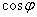
的平方成反比，即
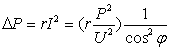
式中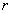
是发电机绕组和线路的电阻。
由上述可知，提高电网的功率因数对国民经济的发展有着极为重要的意义。功率因数的提高，能使发电设备的容量得到充分利用，同时也能使电能得到大量节约。也就是说，在同样的发电设备的条件下能够多发电。
功率因数不高，根本原因就是由于电感性负载的存在。例如生产中最常用的异步电动机在额定负载时的功率因数约为0.7~0.9左右，如果在轻载时其功率因数就更低。其他如工频炉、电焊变压器以及日光灯等负载的功率因数也都是较低的。电感性负载的功率因数之所以小于1，是由于负载本身需要一定的无功功率。从技术经济观点出发，如果解决这个矛盾，也就是如何才能减少电源与负载之间能量的互换，而又使电感性负载能取得所需的无功功率，这就是要提高功率因数的实际意义。
按照供用电规则，高压供电的工业企业的平均功率因数不低于0.95，其他单位不低于0.9。
提高功率因数，常用的方法就是与电感性负载并联静电电容器(设置在用户或变电所中)，其电路图和相量图如图1所示。
 |
 |
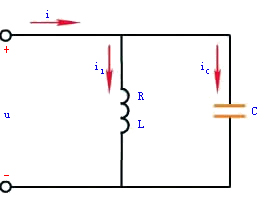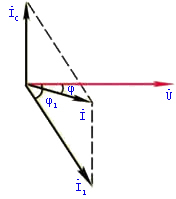| (a)电路图 | (b)相量图 |
|
图1电容器与电感性负载并联以提高功率因数 | |
并联电容器以后，电感性负载的电流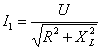
和功率因数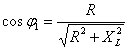
均未变化，这是因为所加电压和负载参数没有改变。但电压
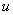和线路电流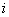
之间的相位差
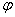变小了，即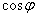
变大了。这里我们所讲的提高功率因数，是指提高电源或电网的功率因数，而不是指提高某个电感性负载的功率因数。
在电感性负载上并联了电容器以后，减少了电源与负载之间的能量互换。这时电感性负载所需的无功功率，大部分或全部都是就地供给(由电容器供给)，就是说能量的互换现在主要或完全发生在电感性负载与电容器之间，因而使发电机容量能得到充分利用。
其次，由相量图可见，并联电容器以后线路电流也减小了(电流相量相加)，因而减小了功率损耗。
应该注意，并联电容器以后有功功率并未改变，因为电容器是不消耗电能的。从相量图上也可看出：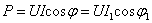
。
功率因素由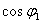
提高到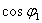
应并联电容器的电容值，可从图1的相量图得出个公式。
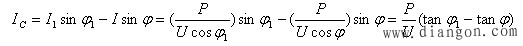
又因
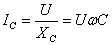
所以
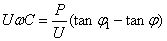
由此得
