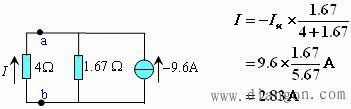
工程实际中,常碰到只需研究某一支路的工作情况。这时,可以将除该支路外的电路其余部分 (通常为一个有源二端网络或称一端口网络),等效变换为较简单的含源支路(电压源与电阻串联或电流源与电阻并联支路),可大大方便分析和计算。
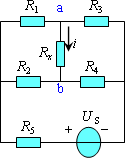
戴维宁定理和诺顿定理正是给出了如何将一个有源线性一端口等效为实际电源模型的分析计算方法。
一、几个名词
1.一端口 (亦称二端网络:two-terminal circuit)
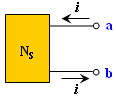
网络与外部电路只有一对端钮连接。
其中从一个端钮(如a)流入的电流一定等于从另一端钮(如b) 流出的电流。
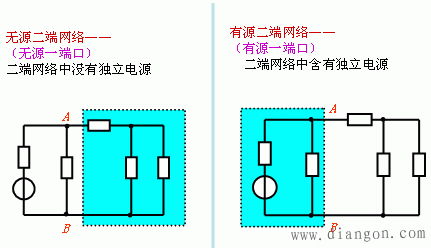
2.含源(active)与无源(passive)一端口网络
网络内部含有独立电源的一端口网络称为含源一端口网络(NS)。
网络内部没有独立电源的一端口网络称为无源一端口网络(N0)。
等效电源定理的概念
有源二端网络用实际电源模型替代,便为等效电源定理。

二、戴维宁定理
1.定义
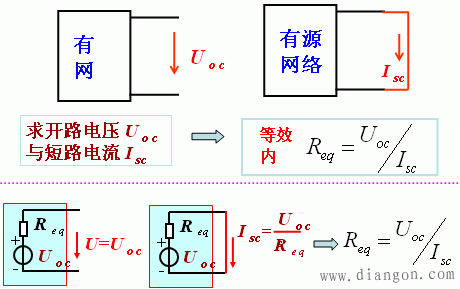
对一个含有独立电源、电阻和受控源的线性一端口网络,对外电路来说,一般可以用一个电压源和电阻的串联组合来等效置换;此电压源的电压等于一端口的开路电压(open-circuit voltage)Uoc,而电阻等于一端口中全部独立电源置零后的输入电阻Req。
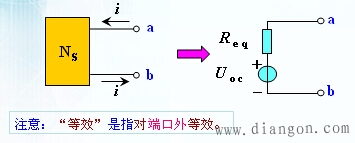
2.戴维宁定理的证明
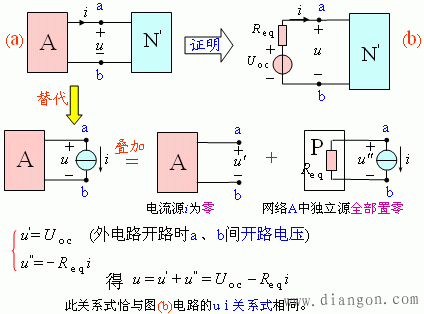
3.等效电源定理中等效电阻的求解方法
(1)无受控源的一端口,其等效内阻Req用电阻串、并联或Y-Δ等效变换的方法即可求出。
例:
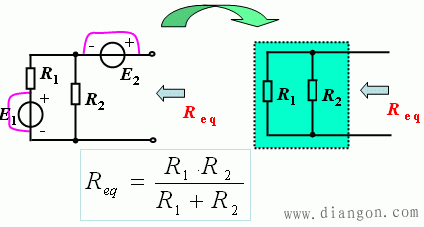
(2)加压求流法或加流求压法
将原有的含源一端口网络NS内所有独立电源均变为零,化为无源一端口网络N0后,在其端口a,b处外施一个电压U,求其端口处的电流I(或者在端口处引入一个电流I,求端口处的两端电压U),则端口处的输入电阻(等效电阻)为:
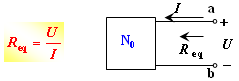
(3)开路电压,短路电流法
例15. 求 a,b 两端的入端电阻 Rab(β≠1)。
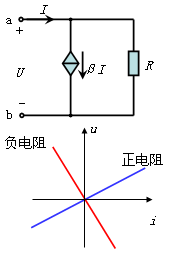
解:通常有两种求入端电阻的方法
① 加压求流法
② 加流求压法
下面用加流求压法求Rab
![]()
![]()
当β<1 , Rab>0,正电阻
当β>1 , Rab<0,负电阻
含受控源的二端网络的输入电阻可能出现负值。具有负值的电阻只是一种电路模型。
例16.
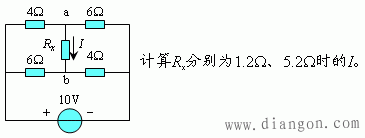
解:保留Rx支路,将其余一端口网络化为戴维宁等效电路:
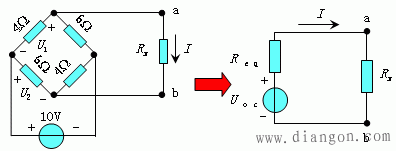
(1)求开路电压
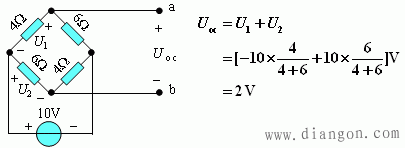
(2)求等效电阻Req
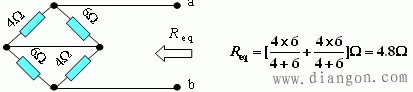
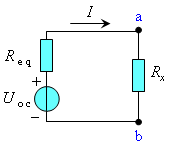
(3)原电路可等效为右图电路,其中:
UOC= 2V
Req= 4.8Ω
(4) Rx = 1.2时,
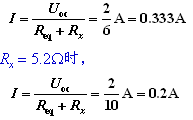
4.含受控源电路戴维南定理的应用
注意: 当一端口内部含有受控源时,其控制电路也必须包含在被化简的一端口中。
例7.
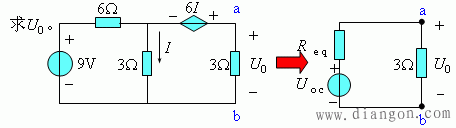
解:(1)求开路电压UOC
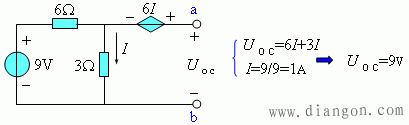
(2) 求等效电阻Req
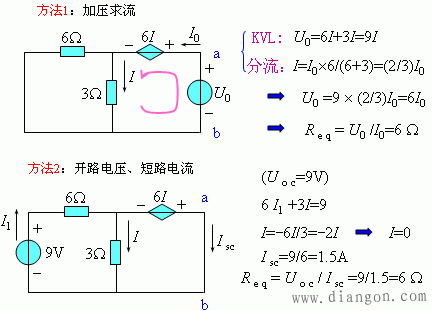
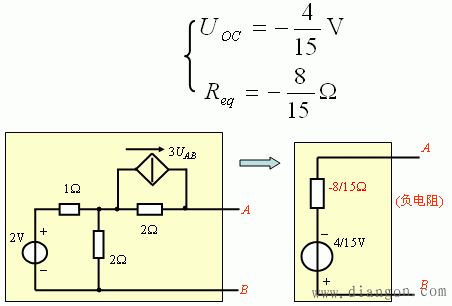
(3) 等效电路
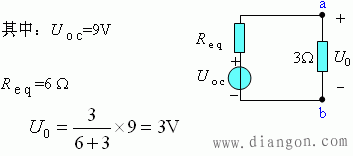
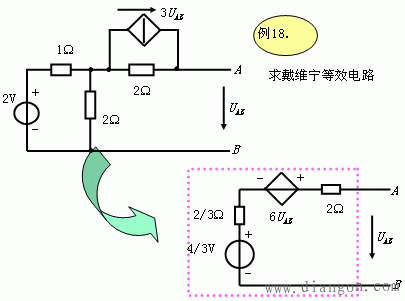
(1) 求开路电压UOC
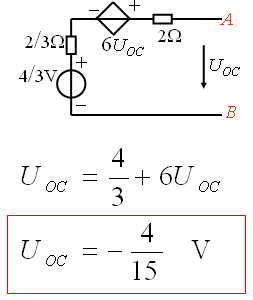
(2) 求输入电阻Req
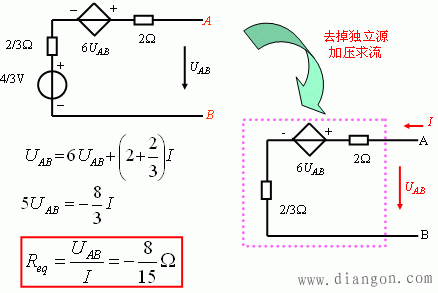
(3) 求等效电路
三、诺顿定理
定义:对于一个含独立电源,线性电阻和线性受控源的一端口网络,对外电路来说,一般可以用一个电流源和电导(电阻)的并联组合来等效置换;电流源的电流等于该含源一端口网络的短路电流(short-circuit current)Isc,而电导(电阻)等于把该一端口网络中的全部独立电源置零后的输入电导Geq(等效电阻Req)。
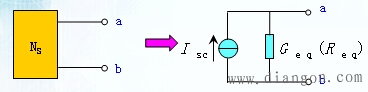
诺顿等效电路可由戴维南等效电路经电源等效变换得到。但须指出,诺顿等效电路可独立进行证明。证明过程从略。
例19. 求电流I 。
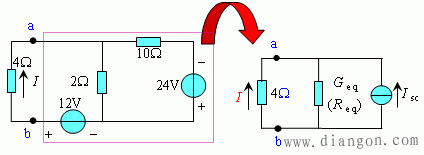
解:(1)求Isc
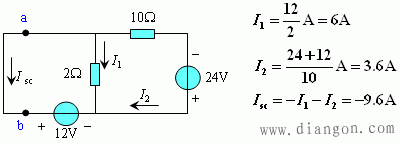
(2) 求Req:串并联
将一端口中全部独立电源置零,即为右图电阻的串并联
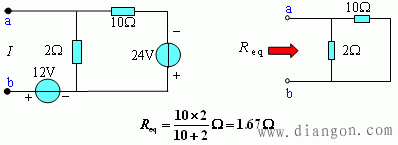
(3) 诺顿等效电路:![]()