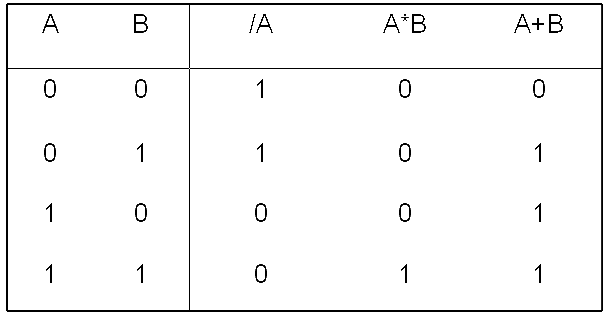
三种基本的门: 所有其它组合逻辑功能都可由这三种门单之产生。
| 逻辑门 | 表示法 | 符号 | 希尔符号 |
| NOT (非) | ā 或 /A | — 或 / (非、负) | |
| AND (与) | A * B | * 与(积) | |
| OR (或) | A+B | + (和) |
二逻辑门等效于
AND 和 NOT : NAND 与非门
OR 和 NT : NOR 或非
任何逻辑功能都可以表示为 “ 与非门 ” 或者 “ 或非门 ” 的功能。
三种基本逻辑门的真值表
运算符的优先级
正常的运算次序是: NOT , AND , OR, 括号中的内容总 是比表达式的其它部分先进行运算。例:

交换律、结合律和分配律
AND 功能和 OR 功能可以交换和结合。
操作数可以任何次序出现,而不会影响功能的运算结果 :
1. 交换律
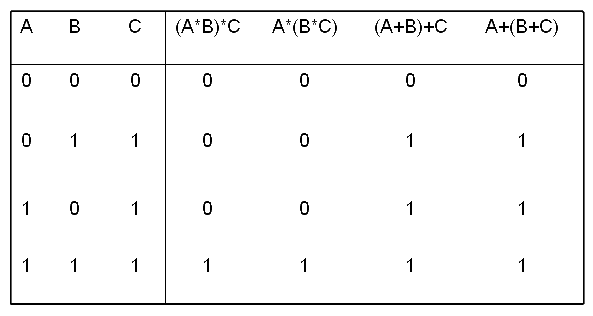
2. 结合律
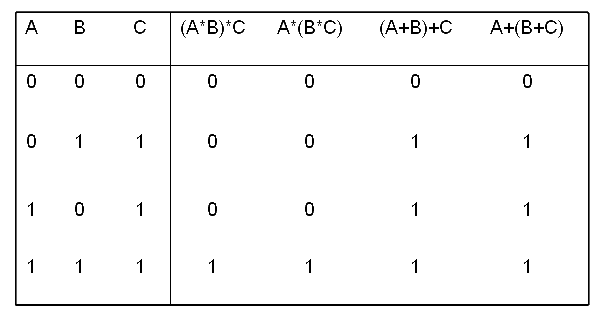
3. 分配律
1. A*(B+C) = (A*B)+(A*C) : 象标准的代数规则 (乘对加)
2. A+(B*C) = (A+B)*(A+C) :真值表或逻辑变换证明 ( 加对乘 )
4.对偶性
对偶性原理:
– 如果用*替换+,+替换*,1替换0,0替换1,则替换后的表达式与 原等式等同。
– 因此只要证明第一条分配律是正确的,通过对偶性就能证明第二 条分配律的正确性。
5 . 逻辑运算的法则
四条基本公理
– 公理 1 : a. X+0=X b. X*0=0
– 公理 2 : a. X+/X=1 b. X*/X=0
– 公理 3 : a. X+Y=Y+X b. X*Y=Y*X
– 公理 4 : a. X*(Y+Z)=(X*Y)+(X*Z) b. X+(Y*Z)=(X+Y) *(X+Z)
九条基本交理
– 定理 1 : a. X+X=X b. X*X=X
– 定理 2 : a. X+1=1 b. X*0=0
– 定理 3 : /(/X)=X ( 不包括具有对偶的元素 + 、 * 、 1 或 0)
– 定理 4 : a. X+(Y+Z)=(X+Y)+Z l b. X*(Y*Z)=(X*Y) *Z
– 定理 5 : a. /(X+Y)=/X*/Y b. /(X*Y)=/X+/Y
– 定理 6 : a. X+(X*Y)=X b. X*(X+Y)=X
– 定理 7 : a. (X+Y)+(X*/Y)=X b. (X+Y) *(X+/Y)=X
– 定理 8 : a. X+(/X*Y)=X+Y b. X*(/X+Y)=X*Y
– 定理 9 : a. (X*Y)+(/X*Z)+(Y*Z)=(X*Y)+(/X*Z) b. (X+Y) *(/X+Z)*(Y*Z)=(X+Y)*(/X+Z)
除定理 3 ,每个定理或公理都有二种形式,属对偶性 原理的关系。
化简时将表示式中所有逻辑变量取非后再写成其对 偶表达形式,即可完成转换:
– 例: /(A*/B+A*C+/A*B*D)
– 第一步取非, /A*B+/A*/C+A*/B*/D
– 第二步取对偶形式, (/A+B)*(/A+C)*(A+/B+/D)
定理 5 ,又称为狄 . 摩根( De Morgan )定理。
