任何复杂的逻辑表达式都可简化为 “ 二级 ” 形式 , 即输 入到输出的二级门电路、 “ 积之和 ” ( SOP )或 “ 和之 积 ” ( POS )。
几个基本概念:
1. 乘积顺 : 一个简单变量或多个变量的逻辑求积,其中变量也可为求补变量
2. 和 项: 一个简单的变量或多个变量的逻辑求和,变量也可为求补变量 。
3. 标准项: 标准项是一个乘积项或和项,其中每一个变量不能使用多 次。
4. 最小项: 最小项是一 个 乘积项,包含每一个变量一次且只有一次 (可以是真值或求补)。
5. 最大项: 最大项是一个和项,它包含每一个变量一次且只有一次 (可以以是真值或求补) 。
6. 积之和表达式: 它是一个乘积项或多个乘积项逻辑求和。
7. 和之积表达式: 它是一个和项或多个 和 项的逻辑求积。
例如:
– A*B*C 乘积项
– A+B+C 和项
– A 既是和项也是积项
– A+B*C 既不是和项也不是积项
– A+ /B 和项 – A*/B*/C 是一个乘积项 l /B 即是和项,也是积项
– /A*B+A*/B 是积之和( SOP )表达式
– (A+B) *(/A+/B) 是和之积( POS )表达式
SOP 或 POS 表达式能直接转化为非常简单的门电路,最简 单的门电路分为两级,信号从输入端到输出端的最长路径 是两个逻辑门电路。
设计逻辑电路时,设计者可把已知变量分为输入、输出两 组,改变输入变量的状态,看看每个输入状态下输出信号 的变化,从而推演出逻辑表达式 , 如。
1 、构造输入、输出直值表
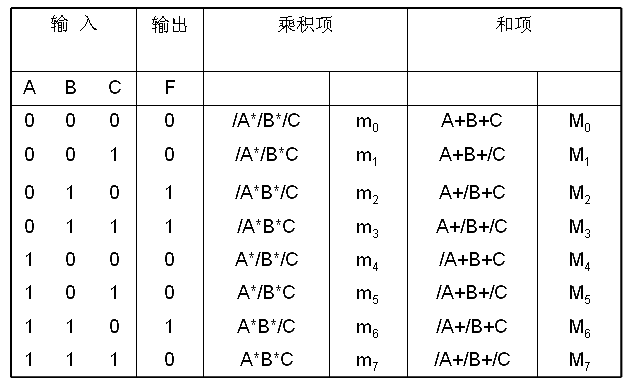
2、推出SOP和POS表达式
将真值表中每个输出为 1 的那些行的乘积项求和,推出 SOP 表达式。
![]()
将真值表中每个输出为 0 的行求积 , 推出 POS 表达式。
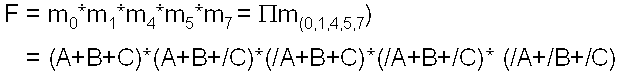
3、简化方程
简化 SOP 方程
F = /A*B*/C + /A*B*C + A*B*/C – = /A*B* (/C + C)+ A*B*/C – = /A*B + A*B*/C – = B*(/A+A*/C) = B*(/A+/C)= /A*B+B*/C
或简化 POS 方程
F = (A+B+C)*(A+B+/C)*(/A+B+C)*(/A+B+/C)* (/A+/B+/C) l = (A+B)*(/A+B)*(/A+/B+/C) l = B*(/A+/C) = /A*B+B*/C
