电路的图

1. 网络图论
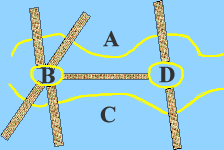
　　图论是拓扑学的一个分支，是富有趣味和应用极为广泛的一门学科。图论的概念由瑞士数学家欧拉最早提出，欧拉在1736年发表的论文《依据几何位置的解题方法》中应用图的方法讨论了各尼斯堡七桥难题，见图1a和b所示。

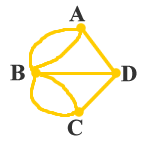图1 a 哥尼斯堡七桥	b 对应的图

　　19～20世纪，图论主要研究一些游戏问题和古老的难题，如哈密顿图及四色问题。1847年，基尔霍夫首先用图论来分析电网络，如今在电工领域，图论被用于网络分析和综合、通讯网络与开关网络的设计、集成电路布局及故障诊断、计算机结构设计及编译技术等等。 2. 电路的图
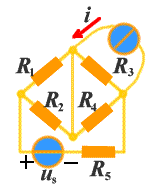
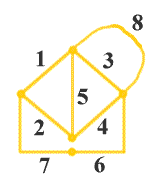
　　电路的图是用以表示电路几何结构的图形，图中的支路和结点与电路的支路和结点一一对应，如图2所示，所以电路的图是点线的集合。通常将电压源与无源元件的串联、电流源与无源元件的并联作为复合支路用一条支路表示。如图2c所示。

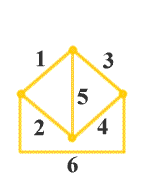a 电路图	b 电路的图(一个元件作为一条支路)	c 电路的图(采用复合支路)
	图2电路和电路的图

　　有向图――标定了支路方向（电流的方向）的图为有向图。
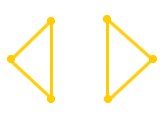
　　连通图――图G的任意两节点间至少有一条路经时称为连通图，非连通图至少存在两个分离部分。

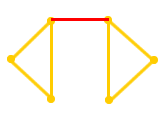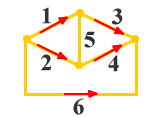
图3 有向图	图4 非连通图	图5 连通图

　　子图――若图G1中所有支路和结点都是图G中的支路和结点，则称G1是图G的子图。

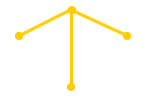a 电路的图（G）	b G图的子图	c G图的子图
	图6

　　树（T）——树（T）是连通图G的一个子图，且满足下列条件：
　　(1) 连通；(2)包含图G中所有结点；(3)不含闭合路径。
　　构成树的支路称树枝；属于图G而不属于树（T）的支路称连支：

图7 电路的图与树的定义

需要指出的是：
　　1）对应一个图有很多的树；
　　2）树支的数目是一定的为结点数减一：b_t=(n-1)
　　3）连枝数为 b_l=b-b_t=b-(n-1)
　　回路――回路L是连通图G的一个子图，构成一条闭合路径，并满足条件：
　　(1)连通；(2)每个节点关联2条支路。
　　需要指出的是：
　　1）对应一个图有很多的回路；
　　2）基本回路的数目是一定的，为连支数；
　　3）对于平面电路，网孔数为基本回路数 l=b_l=b-(n-1)

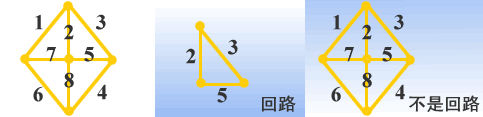图8电路的图与回路定义

　　基本回路(单连支回路)――基本回路具有独占的一条连枝色，即基本回路具有别的回路所没有的一条支路。

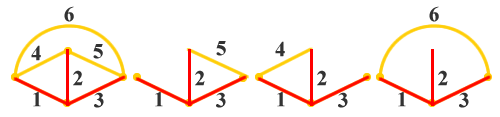图9 电路的图及其基本回路

　　结论：电路中结点、支路和基本回路关系为：支路数＝树枝数＋连支数＝结点数－1＋基本回路数 b=n+l-1