【复数】 复数有三种表示形式，即
直角坐标形式：
极坐标形式：
指数形式：
其中
。它们的互换关系是
【复数运算规则】 复数运算遵循以下规律：
（共轭运算）
【相量（复数）与正弦波】 用相量（复数）来表示正弦波的理论依据是欧拉公式，即
正弦量可表示为
【最大值相量】 令
，上式写为
即是对应于正弦量
的相量，称为最大值相量，它包含了正弦量的幅值和初相信息，不包含正弦量的频率信息。
【有效值相量】 
亦是与正弦量对应的相量，它反映了正弦量的有效值和初相。称
为有效值相量。显然
【旋转相量】 将
画在复平面上，如图8-2-1所示。不难看出，随时间的增长，
是相量
以角度速
逆时针方向旋转的结果，称为旋转相量，旋转相量在实轴上的投影就是正弦量
。
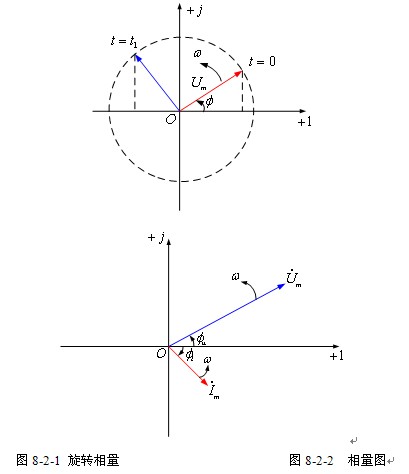
【相量图】 若将同频率的不同正弦量对应的旋转相量画在同一复平面上，例如
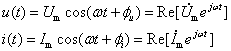
可得图8-2-2，相量和
以相同的频率逆时针方向旋转，保持相对位置不变，这样的图称为相量图。相量图清楚地反映了相量所对应的正弦量的相位关系。图中超前。
综上所述，正弦量和相量构成一一对应的关系。考虑到正弦稳态电路中的所有电量为同频率的正弦量，正弦稳态分析的任务，是确定各电量的幅值和初相，即确定各电量（正弦量）对应的相量，因此将
抛开，仅用相量来建立方程。