同步时序逻辑电路的主要工作特点是,随着时间的推移和外部输入的不断变化,在时钟脉冲作用下电路的状态和输出将发生相应变化。因此,分析的关键是找出电路状态和输出随输入变化而变化的规律,以便确定其逻辑功能。
分析同步时序电路有两种常用的方法,一种是表格法,另一种是代数法。
例如 采用表格法分析图1所示同步时序逻辑电路。
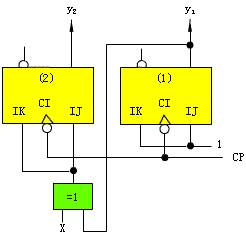
图1
解 由图1可知,该电路的存储电路是两个J-K触发器,组合电路是一个异或门,电路的输入为x,电路的状态y2、y1即电路的输出,因此,它属于Moore型电路的特例。
① 写出输出函数表达式和激励函数表达式
该电路的输出即为状态,故只需写出激励函数表达式。由逻辑电路图可知,各触发器的激励函数表达式为
![]()
② 列出电路的次态真值表
填写次态真值表时,应首先依次列出电路输入和现态的所有取值组合;然后根据激励函数表达式,填写出每一组输入和现态取值下各激励函数的相应函数值;最后,根据表中的现态和激励函数值以及相应触发器的功能表填出每一种输入和现态下的次态。该电路的次态真值表如表1所示。
表1
|
输入 x |
现态 y2 y1 |
激励函数 J2 K2 JI K1 |
次态 |
|
0 0 0 0 1 1 1 1 |
0 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1 |
0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 |
0 1 1 0 1 1 0 0 1 1 0 0 0 1 1 0 |
③ 作出状态表和状态图
根据表5.1所示的次态真值表,可作出该电路的状态表如表2所示,状态图如图2所示。
表2
|
现态 y2 y1 |
次态 | |
| x=0 | x=1 | |
|
0 0 0 1 1 0 1 1 |
0 1 1 0 1 1 0 0 |
1 1 0 0 0 1 1 0 |
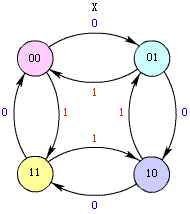
图2
④ 用时间图和文字描述电路的逻辑功能
时间图反映了时序电路在某一给定初始状态下,对典型输入序列的响应。作时间图时,一般先假设电路初始状态并拟定一典型输入序列,然后画出在输入序列作用下状态和输出响应序列的波形图。
设给定电路的初始状态为y2y1=00,输入x为电平信号,典型输入序列为111100000,则根据状态表或状态图可作出电路的时间图如图3所示。
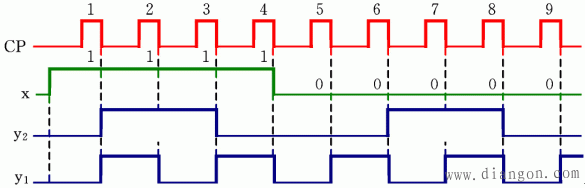
图3
功能:由状态图和时间图可以看出,该电路是一个2位二进制数可逆计数器。当电路输入x=0时,可逆计数器进行加1计数;当输入x=1时,可逆计数器进行减1计数。
