换路定律及初始条件的确定

一、关于换路：为了叙述方便，把引起过渡现象的电路参数、电路结构、电源的变化统称为换路。
二、换路定律解决的问题：
　　求解微分方程必须知道初始条件，数学中的初始条件是给定的，而在电路理论中，是待定的。必须通过换路前的电路状态得到换路后的初始时刻的电路状态，就要建立起换路前后的瞬间，有关物理量之间的关系。
　　为了表达方便，把换路的瞬间记为t=0，换路前的终了时刻记为t=0-，换路后的初始时刻记为t=0+，因此换路定律解决的是换路前后的瞬间有关物理量之间的关系。
三、换路定律：有两条。
（1）对于线性电容：选择电容的端电压u(电荷q)、电流i之间满足关联参考方向，则

(2)对于线性电感：选择电感的电流i与端电压u之间满足关联参考方向或电流与磁链之间满足右螺旋关系，用同样的方法可以证明：

　　结论：在换路的瞬间，如果电容的电流保持为有限值，则电容的电荷、电压保持换路前终了时刻的数值而不能跃变；如果电感的电压保持为有限值，则电感的磁链、电流保持换路前终了时刻的数值而不能跃变。
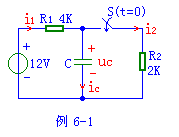
【实例6-1】电路如图例6-1。开关闭合前电路已达到稳态，求换路后的瞬间电容的电压和各支路的电流。　 　　　　　　　　　
【解】各支路电流及电容电压如图示。

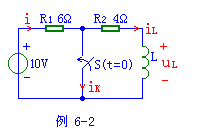
【实例6-2】电路如图例6-2。开关闭合前电路已达到稳态，求换路后的瞬间电感的电压和各支路的电流。

【解】各支路电流及电感电压如图示。