阻抗和导纳的概念以及对它们的运算和等效变换是线性电路正弦稳态分析中的重要内容。
1、阻抗
在如图1(a)所示的正弦稳态电路中,一端口N0的端电压相量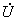 和电流相量
和电流相量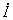 的比值定义为一端口N0的(复)阻抗Z,即有
的比值定义为一端口N0的(复)阻抗Z,即有
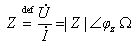 (1)
(1)
上式是用阻抗Z表示的欧姆定律的相量形式。Z不是一个正弦量,而是一个复数,称为复阻抗,其模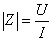 称为阻抗模(经常将Z、
称为阻抗模(经常将Z、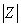 简称为阻抗);辐角
简称为阻抗);辐角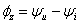 称为阻抗角。阻抗的单位Ω,其电路符号与电阻相同,如图1(b)所示。
称为阻抗角。阻抗的单位Ω,其电路符号与电阻相同,如图1(b)所示。
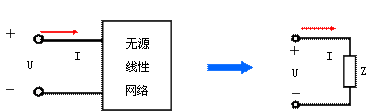
| (a) | (b) |
2、RLC串联电路
正弦稳态电路的RLC串联电路如图2(a)所示,利用相量法将其化为相量模型如图2(b)所示。
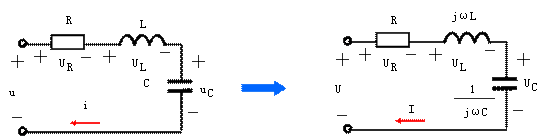
| (a) | (b) |
根据KVL,
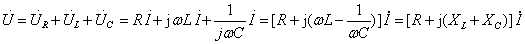
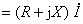
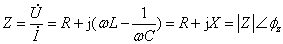 (2)
(2)
式中R为等效电阻分量,X为等效电抗分量。转换关系满足
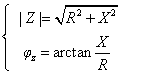 或
或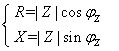 (3)
(3)
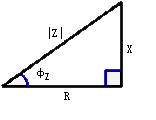
所以阻抗Z可在复平面上用直角三角形表示,如图3所示,称为阻抗三角形。
相量图:在正弦稳态电路中,串联电路一般选电流为参考向量,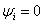 。
。
①当ωL>1/ωC,即X>0时,画出相量图如图4(a)所示,有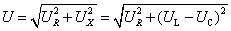 ,此时
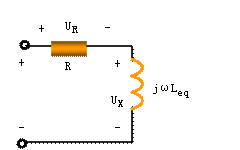
,此时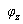 > 0,电路为感性,电压超前电流,该三角形称为电压三角形;等效电路如图4(b)所示。
> 0,电路为感性,电压超前电流,该三角形称为电压三角形;等效电路如图4(b)所示。
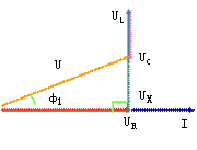 (a)
(a) |
 (b)
(b) |
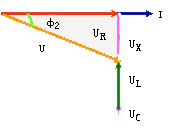
② 当ωL<1/ωC,即X<0时,画出相量图如图5(a)所示,有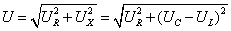 ,此时
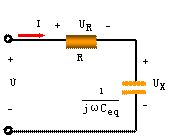
,此时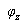 <0,电路为容性,电压滞后电流;等效电路如图5(b)所示。
<0,电路为容性,电压滞后电流;等效电路如图5(b)所示。
 (a)
(a) |
 (b)
(b) |
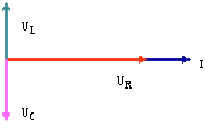
③当ωL=1/ωC,即X = 0时,画出相量图如图6(a)所示,有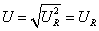 ,此时
,此时 =0,电路为电阻性,电压与电流同相;等效电路如图6(b)所示。
=0,电路为电阻性,电压与电流同相;等效电路如图6(b)所示。
 (a)
(a) |
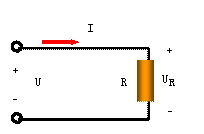 (b)
(b) |
注意
分析 R、L、C串联电路得出:
①ωL>1/ωC,X>0, >0,电路为感性,电压超前电流;
>0,电路为感性,电压超前电流;
②ωL<1/ωC,X<0,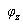 <0,电路为容性,电压落后电流;
<0,电路为容性,电压落后电流;
③ωL=1/ωC,X=0,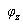 =0,电路为电阻性,电压与电流同相。
=0,电路为电阻性,电压与电流同相。
3、导纳
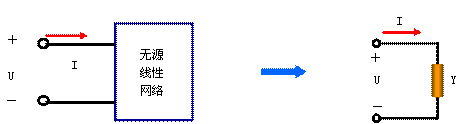
在如图7(a)所示的正弦稳态电路中,一端口N0的电流相量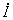 与端电压相量
与端电压相量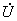 的比值定义为一端口N0的(复)导纳Y,即有
的比值定义为一端口N0的(复)导纳Y,即有
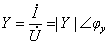 (4)
(4)
上式是用导纳Y表示的欧姆定律的相量形式。Y是一个复数,称为复导纳,其模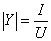 称为导纳模(经常将Y、
称为导纳模(经常将Y、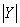 简称为导纳);辐角
简称为导纳);辐角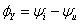 称为导纳角。Y的单位为S西门子,其电路符号与电导相同,如图7(b)所示。
称为导纳角。Y的单位为S西门子,其电路符号与电导相同,如图7(b)所示。
| (a) | (b) |
4、RLC并联电路
正弦稳态电路的RLC并联电路如图8(a)所示,利用相量法将其化为相量模型如图8(b)所示。

| (a) | (b) |
根据KCL,
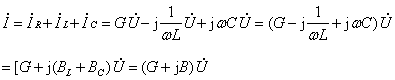
所以,有
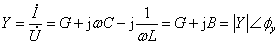 (5)
(5)
式中G为等效电导分量,B为等效电纳分量。转换关系满足
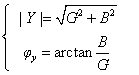 或
或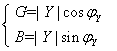 (6)
(6)
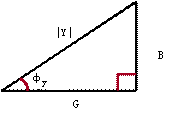
所以导纳Y可在复平面上用直角三角形表示,如图9所示,称为导纳三角形。
相量图:在正弦稳态电路中,并联电路一般选电压为参考向量,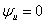 。
。
①当ωC>1/ωL,即B>0时,画出相量图如图10(a)所示,有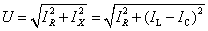 ,此时
,此时 >0,电路为容性,电流超前电压;等效电路如图10(b)所示。
>0,电路为容性,电流超前电压;等效电路如图10(b)所示。
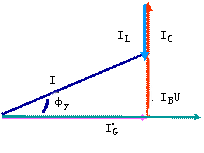 (a)
(a) |
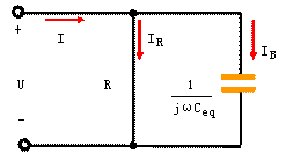 (b)
(b) |
② 当ωC<1/ωL,即B<0时,画出相量图如图11(a)所示,有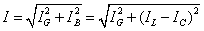 ,此时
,此时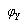 <0,电路为感性,电流滞后电压;等效电路如图11(b)所示。
<0,电路为感性,电流滞后电压;等效电路如图11(b)所示。
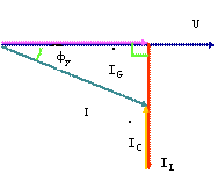 (a)
(a) |
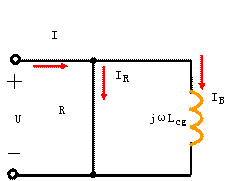 (b)
(b) |
③当ωC=1/ωL,即B =0时,画出相量图如图12(a)所示,此时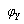 =0,电路为电阻性,电流与电压同相;等效电路如图11(b)所示。
=0,电路为电阻性,电流与电压同相;等效电路如图11(b)所示。
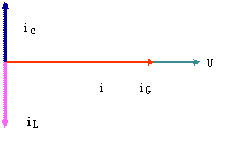 (a)
(a) |
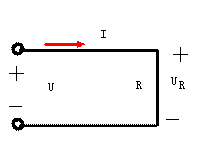 (b)
(b) |
注意
分析 R、L、C并联电路得出:
①ωC>1/ωL,B>0,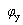 >0,电路为容性,电流超前电压;
>0,电路为容性,电流超前电压;
②ωC<1/ωL,B<0,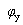 <0,电路为感性,电流滞后电压;
<0,电路为感性,电流滞后电压;
③ωC=1/ωL,B=0,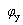 =0,电路为电阻性,电压与电流同相。
=0,电路为电阻性,电压与电流同相。
5、复阻抗和复导纳的等效互换
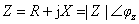 ,
,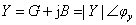 ,Z与Y实现等效变换的条件
,Z与Y实现等效变换的条件
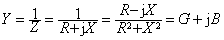
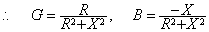
注意
一般情况G≠1/R ,B≠1/X。若Z为感性,X>0,则B<0,即仍为感性。
