1.代入规则 任何一个含有变量X的等式,如果将所有出现 X的位置都代入同一个逻辑函数,则此等式仍然成立。
【例】B(A十C)=BA+BC,现将所有出现A的地方都代入函数F=BC,则有
左式:B(BC十C)=BBC十BC=BC
右式:B B C十B C = B C
2.反演规则 它是使用摩根定律,来求的非函数 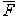
已知一个逻辑函数 F,当求其反函数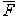 时, ①将 F 表达式中的与(·)换成或(十),或(十)换成与(·);②将原变量换成非变量,非变量换成原变量;③将逻辑1换成0,0换成l。
时, ①将 F 表达式中的与(·)换成或(十),或(十)换成与(·);②将原变量换成非变量,非变量换成原变量;③将逻辑1换成0,0换成l。
在使用反演规则还需注意:仍需遵守“先括号,然后乘,最后加”的运算优先次序;不属于单个变量上的反号应保留不变。
【例】 已知F = A(B + C)+ C D,求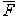 。
。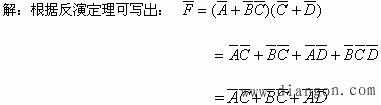
3.对偶规则 如果两个表达式相等,那么它们的对偶式也一定相等,称为对偶规则。 F 是一个逻辑表达式,把F中的与(·)换成或(+),或(+)换成与(·);1换成0,0换成1,所得的新的逻辑函数式叫F的对偶式,记为F'。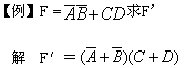
导读:目前正在解读《逻辑代数运算的基本规则》的相关信息,《逻辑代数运算的基本规则》是由用户自行发布的知识型内容!下面请观看由(电工学习网 - www.9pbb.com)用户发布《逻辑代数运算的基本规则》的详细说明。
提醒:《逻辑代数运算的基本规则》最后刷新时间 2023-07-10 03:54:18,本站为公益型个人网站,仅供个人学习和记录信息,不进行任何商业性质的盈利。如果内容、图片资源失效或内容涉及侵权,请反馈至,我们会及时处理。本站只保证内容的可读性,无法保证真实性,《逻辑代数运算的基本规则》该内容的真实性请自行鉴别。
